Question

【题目】如图，已知∠AGE+∠AHF=180°，∠BEC=∠BFC，则∠A与∠D相等吗？下面是童威同学的推导过程，请你帮助他在括号内填上推导依据 ∵∠AGE+∠AHF=180°（已知）
∠AGE=∠CGD （）
∴∠CGD+∠AHF=180°
∴CE∥BF （）
∴∠BEC+∠B=180°
∵∠BFC+∠BFD=180°
∠BEC=∠BFC（已知）
∴∠B=∠BFD （）
∴AB∥CD
∴∠A=∠D．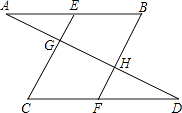

Answer 1

【答案】对顶角相等；同旁内角互补，两直线平行；同角的补角相等
【解析】解：∵∠AGE+∠AHF=180°（已知）， ∠AGE=∠CGD （对顶角相等），
∴∠CGD+∠AHF=180°，
∴CE∥BF （同旁内角互补，两直线平行），
∴∠BEC+∠B=180°，
∵∠BFC+∠BFD=180°，
∠BEC=∠BFC（已知），
∴∠B=∠BFD （同角的补角相等），
∴AB∥CD，
∴∠A=∠D，
所以答案是：对顶角相等，同旁内角互补，两直线平行，同角的补角相等．
【考点精析】掌握平行线的判定与性质是解答本题的根本，需要知道由角的相等或互补（数量关系）的条件，得到两条直线平行（位置关系）这是平行线的判定；由平行线（位置关系）得到有关角相等或互补（数量关系）的结论是平行线的性质．