Question

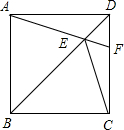
如图，在正方形ABCD中，DC的中点为E，F为CE的中点，求证：∠DAE=

1

2

∠BAF．

Answer 1

证明：如图，作∠BAF的平分线AH交DC的延长线于H，则∠1=∠2=∠3，
∴FA=FH．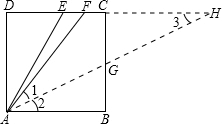
设正方形边长为a，在Rt△ADF中，
AF²=AD²+DF²=a²+（

3a

4

）²=

25

16

a²，
∴AF=

5

4

a=FH．
∴CH=FH-FC=

5

4

a-

a

4

=a，
∴HC=AB．
∵四边形ABCD是正方形，
∴∠B=∠BCD=∠BCH=90°．
在△ABG和△HCG中，

∠B=∠BCH AB=HC ∠2=∠3

∴△ABG≌△HCG（AAS），
∴GB=GC=DE=

1

2

a．
∴∠DAE=∠2=

1

2

∠BAF．