题目内容
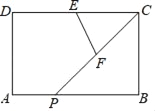
【题目】如图,矩形△ABCD中,AB=2,AD=1,E为CD中点,P为AB边上一动点(含端点),F为CP中点,则△CEF的周长最小值为_____.
【答案】![]() +1.
+1.
【解析】
根据三角形的中位线的性质得到EF=![]() PD,得到C△CEF=CE+CF+EF=CE+
PD,得到C△CEF=CE+CF+EF=CE+![]() (CP+PD)=
(CP+PD)=![]() (CD+PC+PD)=
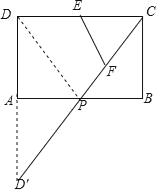
(CD+PC+PD)=![]() C△CDP,当△CDP的周长最小时,△CEF的周长最小;即PC+PD的值最小时,△CEF的周长最小;如图,作D关于AB的对称点D′,连接CD′交AB于P,于是得到结论.
C△CDP,当△CDP的周长最小时,△CEF的周长最小;即PC+PD的值最小时,△CEF的周长最小;如图,作D关于AB的对称点D′,连接CD′交AB于P,于是得到结论.
解:∵E为CD中点,F为CP中点,
∴EF=![]() PD,
PD,
∴C△CEF=CE+CF+EF=CE+![]() (CP+PD)=
(CP+PD)=![]() (CD+PC+PD)=
(CD+PC+PD)=![]() C△CDP,
C△CDP,
∴当△CDP的周长最小时,△CEF的周长最小;
即PC+PD的值最小时,△CEF的周长最小;
如图,作D关于AB的对称点D′,连接CD′交AB于P,
∵AD=AD′=BC,AD′∥BC,
∴四边形AD′BC是平行四边形,
∴AP=PB=1,PD′=PC,
∴CP=PD=![]() ,
,
∴C△CEF=![]() C△CDP=
C△CDP=![]() +1,
+1,
故答案为:![]() +1.
+1.

练习册系列答案
相关题目
【题目】新房装修后,甲居民购买家居用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称 | 单价(元) | 数量(个) | 金额(元) |
挂钟 | 30 | 2 | 60 |
垃圾桶 | 15 | ||
塑料鞋架 | 40 | ||
艺术字画 | a | 2 | 90 |
电热水壶 | 35 | 1 | b |
合计 | 8 | 280 | |
(1)直接写出a= , b=;
(2)甲居民购买了垃圾桶,塑料鞋架各几个?
(3)若甲居民再次购买艺术字画和垃圾桶两种家居用品,共花费150元,则有哪几种不同的购买方案?