题目内容
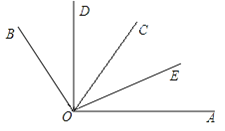
【题目】已知:如图所示,OD平分∠BOC,OE平分∠AOC.若∠BOC=70°,∠AOC=50°.
(1)求出∠AOB及其补角的度数;
(2)求出∠DOC和∠AOE的度数,并判断∠DOE 与∠AOB是否互补,并说明理由;
(3)若∠BOC=α,∠AOC=β,则∠DOE 与∠AOB是否互补,并说明理由.
【答案】(1)∠AOB=120°,其补角为60°;(2)∠DOE=60°,∠AOB=120°,∠DOE与∠AOB互补;(3)∠DOE与∠AOB不互补,理由见解析.
【解析】
(1)由∠AOB=∠BOC+∠AOC,以及补角的定义,即可得到答案;
(2)根据角平分线的定义,即可求出∠DOE和∠AOE的度数,然后∠DOE+∠AOB=180°,即可得到答案;
(3)分别求出∠DOE与∠AOB的度数,然后进行判断,即可得到答案.
解:(1)∠AOB=∠BOC+∠AOC=70°+50°=120°,
其补角为:180°![]() ∠AOB=180°
∠AOB=180°![]() 120°=60°.
120°=60°.
(2)∠DOE与∠AOB互补;
理由如下:∵OD平分∠BOC,OE平分∠AOC,
∴∠DOC=![]() ∠BOC=
∠BOC=![]() ×70°=35°,∠COE=
×70°=35°,∠COE=![]() ∠AOC=
∠AOC=![]() ×50°=25°.
×50°=25°.
∴∠DOE=∠DOC+∠COE =35°+25°=60°.
∴∠DOE+∠AOB=60°+120°=180°,
∴∠DOE与∠AOB互补.
(3)∠DOE与∠AOB不互补,
理由如下:∵OD平分∠BOC,OE平分∠AOC,
∴∠DOC=![]() ∠BOC=
∠BOC=![]() α,∠COE=
α,∠COE=![]() ∠AOC=
∠AOC=![]() β.
β.
∴∠DOE=∠DOC+∠COE =![]() α+
α+![]() β=
β=![]() (α+β).
(α+β).
∴∠DOE+∠AOB=![]() (α+β)+(α+β)=
(α+β)+(α+β)=![]() (α+β),
(α+β),
∴∠DOE与∠AOB不互补.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案【题目】为了解某校八年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:![]() )绘制成不完整的频数分布表和频数分布直方图.
)绘制成不完整的频数分布表和频数分布直方图.
学生立定路远测试成绩的频数分布表
分组 | 频数 |
|
|
| 12 |
|
|
| 10 |
请根据图表中所提供的信息,完成下列问题:
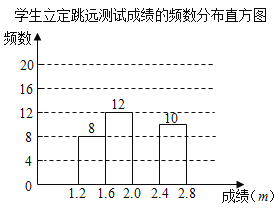
(1)求表中![]() ,
,![]() 的值;
的值;
(2)请把频数分布直方图补充完整;
(3)该校八年级共有800名学生,估计该年级学生立定跳远成绩在![]() 范围内的学生有多少人?
范围内的学生有多少人?