题目内容
【题目】如图，矩形ABCD中，AB=6，BC=8，点E是射线CB上的一个动点，把△DCE沿DE折叠，点C的对应点为C′．
（1）若点C′刚好落在对角线BD上时，BC′=；
（2）若点C′刚好落在线段AB的垂直平分线上时，求CE的长；
（3）若点C′刚好落在线段AD的垂直平分线上时，求CE的长．
【答案】
（1）4
（2）
解：如图2，连接CC′，
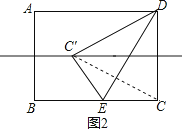
∵点C′在AB的垂直平分线上，
∴点C′在DC的垂直平分线上，
∴CC′=DC′=DC，则△DC′C是等边三角形，
设CE=x，易得DE=2x，
由勾股定理得：（2x）2﹣x2=62，
解得：x=2 
，
即CE的长为2 ；
（3）
解：作AD的垂直平分线，交AD于点M，交BC于点N，分两种情况讨论：
①当点C′在矩形内部时，如图3，
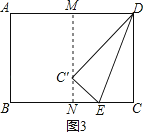
∵点C′在AD的垂直平分线上，
∴DM=4，
∵DC′=6，
由勾股定理得：MC′=2 
，∴NC′=6﹣2 ，
设EC=y，则C′E=y，NE=4﹣y，
故NC′2+NE2=C′E2，
即（6﹣2）2+（4﹣y）2=y2，
解得：y=9﹣3 ，即CE=9﹣3 ；
②当点C′在矩形外部时，如图4，
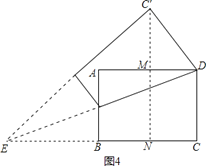
∵点C′在AD的垂直平分线上，
∴DM=4，
∵DC′=6，
由勾股定理得：MC′=2 ，∴NC′=6+2 ，
设EC=z，则C′E=a，NE=z﹣4
故NC′2+NE2=C′E2，
即（6+2 ）2+（z﹣4）2=z2，解得：z=9+3 ，即CE=9+3 ，综上所述：CE的长为9±3 ．
【解析】解：如图1，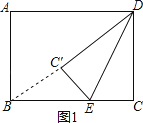
∵点B，C′，D在同一直线上，
∴BC′=BD﹣DC′=BD﹣DC=10﹣6=4；
故答案为：4；
（1）根据点B，C′，D在同一直线上得出BC′=BD﹣DC′=BD﹣DC求出即可；（2）利用垂直平分线的性质得出CC′=DC′=DC，则△DC′C是等边三角形，进而利用勾股定理得出答案；（3）利用①当点C′在矩形内部时，②当点C′在矩形外部时，分别求出即可．
