题目内容
已知方程:①x+ =
= (x-
(x- );②
);② +
+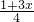 =7-
=7-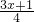 ;③3x-1=2x+1,④
;③3x-1=2x+1,④ x-1=x 中,解为x=2的是方程
x-1=x 中,解为x=2的是方程
- A.①、②和③
- B.①、③和④
- C.②、③和④
- D.①、②和④
C
分析:将x=2分别代入个方程的左右两边进行验证,如果左右两边相等,则是方程的解,否则不是.
解答:当x=2时,
①∵左边=x+ =2+
=2+ =
= ,右边=
,右边= (x-
(x- )=
)= ×(2-
×(2- )=1,
)=1,
∴左边≠右边,
∴x=2的不是方程的解;
②∵左边= +
+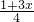 =
= +
+ =
=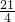 ,右边=7-
,右边=7-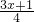 =7-
=7-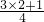 =
=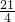 ,
,
∴左边=右边,
∴x=2的是方程的解;
③∵左边=3x-1=3×2-1=5,右边=2x+1=2×2+1=5,
∴左边=右边,
∴x=2的是方程的解;
④∵左边= x-1=
x-1= ×2-1=2,右边=2,
×2-1=2,右边=2,
∴左边=右边,
∴x=2的是方程的解.
∴②③④的解为x=2.
故选C.
点评:此题考查了方程与方程的解的关系:方程的解能使得方程左右两边相等.题目比较简单,解题时要细心.
分析:将x=2分别代入个方程的左右两边进行验证,如果左右两边相等,则是方程的解,否则不是.
解答:当x=2时,
①∵左边=x+
 =2+
=2+ =
= ,右边=
,右边= (x-
(x- )=
)= ×(2-
×(2- )=1,
)=1,∴左边≠右边,
∴x=2的不是方程的解;
②∵左边=
 +
+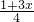 =
= +
+ =
=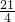 ,右边=7-
,右边=7-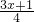 =7-
=7-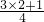 =
=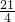 ,
,∴左边=右边,
∴x=2的是方程的解;
③∵左边=3x-1=3×2-1=5,右边=2x+1=2×2+1=5,
∴左边=右边,
∴x=2的是方程的解;
④∵左边=
 x-1=
x-1= ×2-1=2,右边=2,
×2-1=2,右边=2,∴左边=右边,
∴x=2的是方程的解.
∴②③④的解为x=2.
故选C.
点评:此题考查了方程与方程的解的关系:方程的解能使得方程左右两边相等.题目比较简单,解题时要细心.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目