题目内容
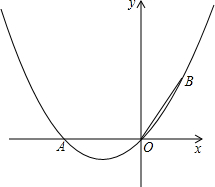 如图,在直角坐标系中,点A的坐标为(-2,0),连接OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.
如图,在直角坐标系中,点A的坐标为(-2,0),连接OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.(1)求点B的坐标;
(2)求经过A、O、B三点的抛物线的解析式;
(3)在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;
(4)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由.
(注意:本题中的结果均保留根号).
分析:(1)由已知得OA=2,将线段OA绕原点O顺时针旋转120°,则OB与x轴的正方向夹角为60°,过点B作BD⊥x轴于点D,解直角三角形可得OD、BD的长,可表示B点的坐标;
(2)直接将A、O、B三点坐标代入抛物线解析式的一般式,可求解析式;
(3)因为点A,O关于对称轴对称,连接AB交对称轴于C点,C点即为所求,求直线AB的解析式,再根据C点的横坐标值,求纵坐标;
(4)设P(x,y)(-2<x<0,y<0),用割补法可表示△PAB的面积,根据面积表达式再求取最大值时,x的值.
(2)直接将A、O、B三点坐标代入抛物线解析式的一般式,可求解析式;
(3)因为点A,O关于对称轴对称,连接AB交对称轴于C点,C点即为所求,求直线AB的解析式,再根据C点的横坐标值,求纵坐标;
(4)设P(x,y)(-2<x<0,y<0),用割补法可表示△PAB的面积,根据面积表达式再求取最大值时,x的值.
解答: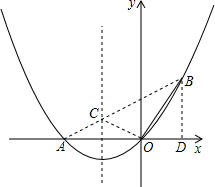 解:(1)过点B作BD⊥x轴于点D,由已知可得:OB=OA=2,∠BOD=60°,
解:(1)过点B作BD⊥x轴于点D,由已知可得:OB=OA=2,∠BOD=60°,
在Rt△OBD中,∠ODB=90°,∠OBD=30°
∴OD=1,DB=
∴点B的坐标是(1,
).(2分)
(2)设所求抛物线的解析式为y=ax2+bx+c(a≠0),
由已知可得:
,
解得:a=
,b=
,c=0,
∴所求抛物线解析式为y=
x2+
x.(4分)
(3)存在,
由y=
x2+
x配方后得:y=
(x+1)2-
∴抛物线的对称轴为x=-1(6分)
(也可用顶点坐标公式求出)
∵点C在对称轴x=-1上,△BOC的周长=OB+BC+CO;
∵OB=2,要使△BOC的周长最小,必须BC+CO最小,
∵点O与点A关于直线x=-1对称,有CO=CA
△BOC的周长=OB+BC+CO=OB+BC+CA
∴当A、C、B三点共线,即点C为直线AB与抛物线对称轴的交点时,BC+CA最小,此时△BOC的周长最小.
设直线AB的解析式为y=kx+b,则有:
,
解得:k=
,b=
,
∴直线AB的解析式为y=
x+
,(7分)
当x=-1时,y=
,
∴所求点C的坐标为(-1,
),(8分)
(4)设P(x,y)(-2<x<0,y<0),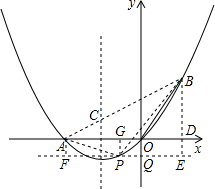
则y=
x2+
x①
过点P作PQ⊥y轴于点Q,PG⊥x轴于点G,过点A作AF⊥PQ轴于点F,过点B作BE⊥PQ轴于点E,
则PQ=-x,PG=-y,
由题意可得:S△PAB=S梯形AFEB-S△AFP-S△BEP(9分)
=
(AF+BE)•FE-
AF•FP-
PE•BE
=
(-y+
-y)(1+2)-
(-y)(x+2)-
(1-x)(
-y)
=-
y+
x+
②
将①代入②,
化简得:S△PAB=-
x2-
x+
(10分)
=-
(x+
)2+
∴当x=-
时,△PAB得面积有最大值,最大面积为
.(11分)
此时y=
×
+
×(-
)=-
∴点P的坐标为(-
,-
).(12分)
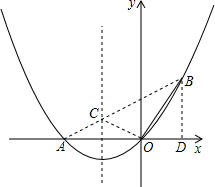 解:(1)过点B作BD⊥x轴于点D,由已知可得:OB=OA=2,∠BOD=60°,
解:(1)过点B作BD⊥x轴于点D,由已知可得:OB=OA=2,∠BOD=60°,在Rt△OBD中,∠ODB=90°,∠OBD=30°
∴OD=1,DB=
| 3 |
∴点B的坐标是(1,
| 3 |
(2)设所求抛物线的解析式为y=ax2+bx+c(a≠0),
由已知可得:
|
解得:a=
| ||
| 3 |
2
| ||
| 3 |
∴所求抛物线解析式为y=
| ||
| 3 |
2
| ||
| 3 |
(3)存在,
由y=
| ||
| 3 |
2
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
∴抛物线的对称轴为x=-1(6分)
(也可用顶点坐标公式求出)
∵点C在对称轴x=-1上,△BOC的周长=OB+BC+CO;
∵OB=2,要使△BOC的周长最小,必须BC+CO最小,
∵点O与点A关于直线x=-1对称,有CO=CA
△BOC的周长=OB+BC+CO=OB+BC+CA
∴当A、C、B三点共线,即点C为直线AB与抛物线对称轴的交点时,BC+CA最小,此时△BOC的周长最小.
设直线AB的解析式为y=kx+b,则有:
|
解得:k=
| ||
| 3 |
2
| ||
| 3 |
∴直线AB的解析式为y=
| ||
| 3 |
2
| ||
| 3 |
当x=-1时,y=
| ||
| 3 |
∴所求点C的坐标为(-1,
| ||
| 3 |
(4)设P(x,y)(-2<x<0,y<0),
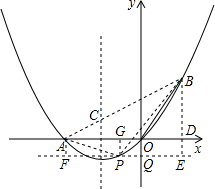
则y=
| ||
| 3 |
2
| ||
| 3 |
过点P作PQ⊥y轴于点Q,PG⊥x轴于点G,过点A作AF⊥PQ轴于点F,过点B作BE⊥PQ轴于点E,
则PQ=-x,PG=-y,
由题意可得:S△PAB=S梯形AFEB-S△AFP-S△BEP(9分)
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
=-
| 3 |
| 2 |
| ||
| 2 |
| 3 |
将①代入②,
化简得:S△PAB=-
| ||
| 2 |
| ||
| 2 |
| 3 |
=-
| ||
| 2 |
| 1 |
| 2 |
9
| ||
| 8 |
∴当x=-
| 1 |
| 2 |
9
| ||
| 8 |
此时y=
| ||
| 3 |
| 1 |
| 4 |
2
| ||
| 3 |
| 1 |
| 2 |
| ||
| 4 |
∴点P的坐标为(-
| 1 |
| 2 |
| ||
| 4 |
点评:本题考查了坐标系中点的坐标求法,抛物线解析式的求法,根据对称性求线段和最小的问题,也考查了在坐标系里表示面积及求面积最大值等问题;
解答本题(4)也可以将直线AB向下平移至与抛物线相切的位置,联立此时的直线解析式与抛物线解析式,可求唯一交点P的坐标.
解答本题(4)也可以将直线AB向下平移至与抛物线相切的位置,联立此时的直线解析式与抛物线解析式,可求唯一交点P的坐标.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: