题目内容

如图所示．E，F分别是?ABCD的边AD，AB上的点，且BE=DF，BE与DF交于O．求证：C点到BE的距离等于它到DF的距离．
连接CF，CE．

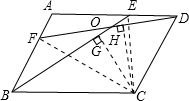
∵S△BCE=S△BCD=
1
2
S?ABCD，
S△CDF=S△CAD=
1
2
S?ABCD，
∴S△BCE=S△CDF．
∵BE=DF，
∴CG=CH（CG，CH分别表示BE，DF上的高），
即C点到BE和DF的距离相等．
练习册系列答案
相关题目
阅读：D为△ABC中BC边上一点，连接AD，E为AD上一点．
如图1，当D为BC边的中点时，有S△EBD=S△ECD，S△ABE=S△ACE；
当
BD
DC
=m时，有
S△EBD
S△ECD
=
S△ABE
S△ACE
=m．
解决问题：
在△ABC中，D为BC边的中点，P为AB边上的任意一点，CP交AD于点E、设△EDC的面积为S1，△APE的面积为S2．
（1）如图2，当
BP
AP
=1时，
S1
S2
的值为______；
（2）如图3，当
BP
AP
=n时，
S1
S2
的值为______；
（3）若S△ABC=24，S2=2，则
BP
AP
的值为______．
如图，AD为△ABC的中线，若△ABC的面积为40，AB=8，则D点到AB边的距离为______．
如图，△ABC的面积为1．分别倍长AB，BC，CA得到△A1B1C1．再分别倍长A1B1，B1C1，C1A1得到△A2B2C2．…按此规律，倍长n次后得到的△AnBnCn的面积为______．
在梯形ABCD中，AB∥CD，对角线AC、BD交于点O，CD=2，AB=5，则S△BOC：S△ADC=（　　）
A．2：5B．5：2C．2：7D．5：7
阅读下面资料：
小明遇到这样一个问题：如图1，对面积为a的△ABC逐次进行以下操作：分别延长AB、BC、CA至A1、B1、C1，使得A1B=2AB，B1C=2BC，C1A=2CA，顺次连接A1、B1、C1，得到△A1B1C1，记其面积为S1，求S1的值．
小明是这样思考和解决这个问题的：如图2，连接A1C、B1A、C1B，因为A1B=2AB，B1C=2BC，C1A=2CA，根据等高两三角形的面积比等于底之比，所以S△A1BC=S△B1CA=S△C1AB=2S△ABC=2a，由此继续推理，从而解决了这个问题．

（1）直接写出S1=______（用含字母a的式子表示）．
请参考小明同学思考问题的方法，解决下列问题：
（2）如图3，P为△ABC内一点，连接AP、BP、CP并延长分别交边BC、AC、AB于点D、E、F，则把△ABC分成六个小三角形，其中四个小三角形面积已在图上标明，求△ABC的面积．
（3）如图4，若点P为△ABC的边AB上的中线CF的中点，求S△APE与S△BPF的比值．
如图，△ABC内三个小三角形的面积分别为5、8、10，则△ABC的面积为______．
△ABC的面积是1平方厘米，如图所示，AD=DE=EC，BG=GF=FC，求阴影四边形的面积．
若从长度分别为2cm、3cm、4cm、6cm的四根木棒中，任意选取三根首尾顺次相连搭成三角形，则搭成的不同三角形共有（　　）
A．1个B．2个C．3个D．4个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网