题目内容
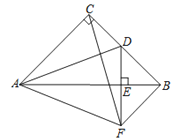
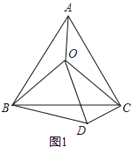
【题目】(1)如图1,O是等边△ABC内一点,连接OA、OB、OC,且OA=3,OB=4,OC=5,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.求:
①旋转角是____度;
②线段OD的长为_____;
③求∠BDC的度数.
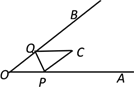
(2)如图2所示,O是等腰直角△ABC(∠ABC=90°)内一点,连接OA、OB、OC,∠A0B=135,OA=1,0B=2,求0C的长.
小明同学借用了图1的方法,将△BAO绕点B顺时针旋转后得到△BCD,请你继续用小明的思路解答,或是选择自己的方法求解.

【答案】(1)①60°;②4;③∠BDC=150°;(2)OC=3.
【解析】试题分析:
(1)①由题意可知旋转角是∠ABC结合△ABC是等边三角形可得旋转角为60°;
②由旋转的性质可知BD=BO,∠OBD=60°,由此可得△OBD是等边三角形,从而可得OD=OB=4;
③由旋转的性质可得CD=OA=3,结合OC=5,OD=4可证得△ODC是直角三角形,∠ODC=90°,结合△OBD是等边三角形可得∠BDC=150°;
(2)由旋转的性质易得BD=BO=2,∠DBO=∠CBA=90°,∠BDC=∠BOA=135°,CD=AO=1,由此可得△DBO是等腰直角三角形,从而可得∠BDO=45°,则∠ODC=90°,这样在Rt△ODC中,由勾股定理即可求得OC的长了.
试题解析:
(1)①由题意可知,旋转角是∠ABC,
∵△ABC是等边三角形,
∴∠ABC=60°,
∴旋转角的度数为60°;
②由旋转的性质可知BD=BO,∠OBD=60°,
∴△OBD是等边三角形,
∴OD=OB=4;
③∵△BOD为等边三角形,
∴∠BDO=60°,OD=4
∵△BAO绕点B顺时针旋转后得到△BCD,
∴CD=AO=3,
在△OCD中,CD=3,OD=4,OC=5,
∵CD2+OD2=32+42=52=OC2,
∴△OCD为直角三角形,∠ODC=90°,
∴∠BDC=∠BDO+∠ODC=60°+90°=150°;
(2)OC=3.
理由如下:
∵△BAO绕点B顺时针旋转后得到△BCD,
∴∠OBD=∠ABC=90°,BO=BD=2,CD=AO=1,
∴△OBD为等腰直角三角形,
∴∠BDO=45°,OD=![]() OB=2
OB=2![]() ,
,
∵△BAO绕点B顺时针旋转后得到△BCD,
∴∠AOB=∠BDC=135°,
∴∠ODC=90°,
∴CD2+OD2=OC2,
∴OC=3.

 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案