题目内容
【题目】已知C为线段AB的中点,E为线段AB上的点,点D为线段AE的中点.
(1)若线段AB=a,CE=b,|a﹣15|+(b﹣4.5)2=0,求a,b的值;
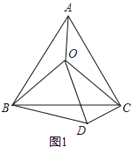
(2)如图1,在(1)的条件下,求线段DE的长;
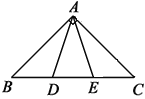
(3)如图2,若AB=15,AD=2BE,求线段CE的长.
![]()
【答案】(1) a=15,b=4.5;(2)6;(3)4.5
【解析】
(1)由|a-15|+(b-4.5)2=0,根据非负数的性质即可推出a、b的值;
(2)根据(1)所推出的结论,即可推出AB和CE的长度,根据图形即可推出AC=7.5,然后由AE=AC+CE,即可推出AE的长度,由D为AE的中点,即可推出DE的长度;
(3)首先设EB=x,根据线段中点的性质推出AD、DE关于x的表达式,即AD=DE=2x,由图形推出AD+DE+BE=15,即可得方程:x+2x+2x=15,通过解方程推出x=3,即BE=3,最后由BC=7.5,即可求出CE的长度.
解:(1)∵|a﹣15|+(b﹣4.5)2=0,∴|a﹣15|=0,(b﹣4.5)2=0,
∵a.b均为非负数,∴a=15,b=4.5,
(2)∵点C为线段AB的中点,AB=15,CE=4.5,∴AC=![]() AB=7.5,∴AE=AC+CE=12,
AB=7.5,∴AE=AC+CE=12,
∵点D为线段AE的中点,∴DE=![]() AE=6,
AE=6,
(3)设EB=x,则AD=2BE=2x,∵点D为线段AE的中点,∴AD=DE=2x,
∵AB=15,∴AD+DE+BE=15,∴x+2x+2x=15,解方程得:x=3,即BE=3,
∵AB=15,C为AB中点,∴BC=![]() AB=7.5,∴CE=BC﹣BE=7.5﹣3=4.5.
AB=7.5,∴CE=BC﹣BE=7.5﹣3=4.5.

练习册系列答案
相关题目