题目内容
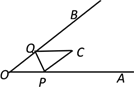
【题目】如图,已知∠AOB=45°,点P、Q分别是边OA,OB上的两点,将∠O沿PQ折叠,点O落在平面内点C处.若折叠后PC⊥QB,则∠OPQ的度数是____________.
【答案】22.5°或112.5°
【解析】分析:根据题意画出符合要求的图形,如下图1和图2,分点C在OA下方和OB上方两种情况结合折叠的性质及已知条件解答即可.
详解:
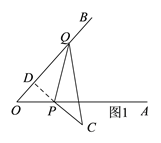
(1)如图1,当点C在OA的下方时,延长CP交OB于点D,
∵CP⊥OB,
∴∠ODC=90°,
∵∠AOB=45°,
∴∠DPC=45°,
∴∠OPQ+∠CPQ=45°+180°=225°,
∵由折叠的性质可知∠OPQ=∠CPQ,
∴∠OPQ=112.5°;
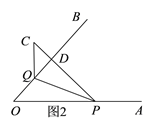
(2)如图2,当点C在OB的上方时,
∵PC⊥OB,
∴∠ODP=90°,
又∵∠AOB=45°,
∴∠OPQ+∠CPQ=∠OPC=45°,
∵由折叠的性质可知∠OPQ=∠CPQ,
∴∠OPQ=22.5°.
综上所述,当PC⊥OB时,∠OPQ的度数为112.5°或22.5°.
故答案为:112.5°或22.5°.

练习册系列答案
相关题目