题目内容
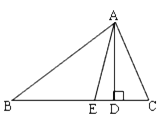
【题目】如图所示,△ABC中,AD⊥BC,AE平分∠BAC.
(1)若∠B=40°,∠C=70°,求∠DAE的度数,并说明理由;
(2)若∠B=α,∠C=β(α<β),请你根据(1)问的结果大胆猜想∠DAE与α,β间的等量关系 .(不需说明理由)
【答案】(1)15°;(2)![]()
【解析】
(1)利用三角形的内角和定理求出∠BAC,再利用角平分线定义求∠BAD,最后求出∠DAE的度数,即可解答;
(2)根据三角形内角和等于180°,所以∠BAC=180°-∠B-∠C,因为AE平分∠BAC,利用∠BAD=90°-∠B,可得结论.
解:(1)∵∠C=70°,∠B=40°,
∴∠BAC=180°-(∠B+∠C)=180°-40°-70°=70°,
∵AE平分∠BAC,
∴∠CAE=![]() ∠BAC=35°
∠BAC=35°
∵AD⊥BC,
∴∠ADC=90°,
∵∠C=70°,
∴∠DAC=90°-70°=20°,
∴∠DAE=∠CAE-∠CAD=35°-20°=15°;
(2) ![]() ,
,
理由:∵AE为角平分线,
∴∠BAE=![]() ,
,
∵AD⊥BC,
∴∠BAD=90°-∠B,
∴∠DAE=∠BAD-∠BAE
=90°-∠B-![]()
==![]()
=![]() .
.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目