题目内容
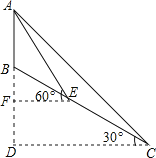
【题目】在学习解直角三角形以后，某兴趣小组测量了旗杆的高度．如图，某一时刻，旗杆AB的影子一部分落在水平地面L的影长BC为5米，落在斜坡上的部分影长CD为4米．测得斜CD的坡度i＝1：
．太阳光线与斜坡的夹角∠ADC＝80°，则旗杆AB的高度_____．（精确到0.1米）（参考数据：sin50°＝0.8，tan50°＝1.2，＝1.732）
【答案】12.2m．
【解析】
延长AD交BC的延长线于点E，作DF⊥CE于点F．解直角三角形求出EF，CF，即可解决问题．
延长AD交BC的延长线于点E，作DF⊥CE于点F．
在△DCF中，∵CD＝4m，DF：CF＝1：
，
∴tan∠DCF＝
，
∴∠DCF＝30°，∠CDF＝60°．
∴DF＝2（m），CF＝2（m），
在Rt△DEF中，因为∠DEF＝50°，
所以EF＝
≈1.67（m）
∴BE＝EF+FC+CB＝1.67+2+5≈10.13（m），
∴AB＝BEtan50°≈12.2（m），
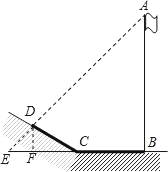
故答案为12.2m．
练习册系列答案
相关题目
【题目】问题：探究函数y＝x+
的图象和性质．
小华根据学习函数的方法和经验，进行了如下探究，下面是小华的探究过程，请补充完整：
（1）函数的自变量x的取值范围是：____；
（2）如表是y与x的几组对应值，请将表格补充完整：
x | … | ﹣3 | ﹣2 | ﹣ | ﹣1 |
|
| 1 |
| 2 | 3 | … |
y | … | ﹣3 | ﹣3 |
| ﹣3 | ﹣4 | 4 |
| 3 | … |
（3）如图，在平面直角坐标系中描点并画出此函数的图象；
（4）进一步探究：结合函数的图象，写出此函数的性质（一条即可）．
