题目内容
 已知,如图,直线MN交⊙O于A、B两点,AC是直径,DE切⊙O于D,DE⊥MN于E.
已知,如图,直线MN交⊙O于A、B两点,AC是直径,DE切⊙O于D,DE⊥MN于E.(1)求证:AD平分∠CAM.
(2)若DE=8cm,AE=4cm,求⊙O的半径.
分析:(1)由DE与圆O相切,利用切线的性质得到OD垂直于DE,再由DE垂直于MB,得到一对同旁内角互补,利用同旁内角互补两直线平行,得到OD与MB平行,利用两直线平行得到一对内错角相等,再由OD=OA,利用等边对等角得到一对角相等,等量代换可得出∠DAE=∠OAD,即AD为∠CAE的平分线,得证;
(2)过O作OF垂直于MB,显然得到四边形ODEF为矩形,利用矩形的对边相等得到OD=EF,OF=DE,设圆的半径为rcm,由DE的长得出OF的长,由EF-AE=OD-EF表示出AF的长,在直角三角形AOF中,利用勾股定理列出关于r的方程,求出方程的解即可得到半径r的长.
(2)过O作OF垂直于MB,显然得到四边形ODEF为矩形,利用矩形的对边相等得到OD=EF,OF=DE,设圆的半径为rcm,由DE的长得出OF的长,由EF-AE=OD-EF表示出AF的长,在直角三角形AOF中,利用勾股定理列出关于r的方程,求出方程的解即可得到半径r的长.
解答: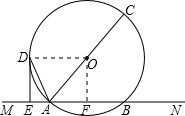 解:(1)证明:连接OD,
解:(1)证明:连接OD,
∵DE切圆O于D,
∴OD⊥DE,
∴∠ODE=90°,
又∵DE⊥MB,
∴∠DEB=90°,
∴∠ODE+∠DEB=180°,
∴OD∥MB,
∴∠ODA=∠DAE,
又∵OD=OA,
∴∠ODA=∠OAD,
∴∠DAE=∠OAD,
则AD为∠CAM的平分线;
(2)过O作OF⊥AB,显然四边形ODEF为矩形,
则OF=DE,OD=EF,
设圆的半径OD=EF=OA=rcm,由DE=8cm,AE=4cm,
得到OF=8cm,AF=EF-AE=(r-4)cm,
在Rt△AOF中,根据勾股定理得:OA2=AF2+OF2,即r2=(r-4)2+82,
整理得:8r=80,
解得:r=10cm.
 解:(1)证明:连接OD,
解:(1)证明:连接OD,∵DE切圆O于D,
∴OD⊥DE,
∴∠ODE=90°,
又∵DE⊥MB,
∴∠DEB=90°,
∴∠ODE+∠DEB=180°,
∴OD∥MB,
∴∠ODA=∠DAE,
又∵OD=OA,
∴∠ODA=∠OAD,
∴∠DAE=∠OAD,
则AD为∠CAM的平分线;
(2)过O作OF⊥AB,显然四边形ODEF为矩形,
则OF=DE,OD=EF,
设圆的半径OD=EF=OA=rcm,由DE=8cm,AE=4cm,
得到OF=8cm,AF=EF-AE=(r-4)cm,
在Rt△AOF中,根据勾股定理得:OA2=AF2+OF2,即r2=(r-4)2+82,
整理得:8r=80,
解得:r=10cm.
点评:此题考查了切线的性质,勾股定理,平行线的判定与性质,利用了转化及方程的思想,熟练掌握切线的性质是解本题的关键.

练习册系列答案
相关题目
 已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E. (2013•路北区三模)已知:如图,直线MN交⊙O于A、B两点,AC是直径,AD平分∠CAM交⊙O于点D,过点D作DE⊥MN,垂足为E.
(2013•路北区三模)已知:如图,直线MN交⊙O于A、B两点,AC是直径,AD平分∠CAM交⊙O于点D,过点D作DE⊥MN,垂足为E. 交于点G,垂足分别是E、F,AC是⊙O的弦,
交于点G,垂足分别是E、F,AC是⊙O的弦, 已知:如图,直线MN交⊙O于A、B两点,AC是直径,AD平分∠CAM交⊙O于点D,过点D作DE⊥MN,垂足为E.∠ADE=30°,⊙O的半径为2,图中阴影部分的面积为
已知:如图,直线MN交⊙O于A、B两点,AC是直径,AD平分∠CAM交⊙O于点D,过点D作DE⊥MN,垂足为E.∠ADE=30°,⊙O的半径为2,图中阴影部分的面积为