题目内容
【题目】(本题8分)如图,矩形ABCD中,AB=2,BC=5,E、P分别在AD、BC上,且DE=BP=1.
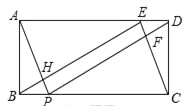
(1)断⊿BEC的形状,并说明理由;
(2)判断四边形EFPH是什么特殊四边形?并证明你的判断。
【答案】(1)△BEC是直角三角形,理由见解析;
(2)四边形EFPH为矩形,证明见解析;
【解析】
试题分析:(1)由矩形性质得出CD=2,根据勾股定理求出CE和BE,求出CE2+BE2的值,求出BC2,根据勾股定理的逆定理求出即可;
(2)由矩形的性质和平行四边形的判定,推出平行四边形DEBP和AECP,推出EH∥FP,EF∥HP,推出平行四边形EFPH,根据矩形的判定推出即可;
试题解析:(1)△BEC是直角三角形,
理由是:∵矩形ABCD,
∴∠ADC=∠ABP=90°,AD=BC=5,AB=CD=2,
由勾股定理得:CE=![]() ,
,
同理BE=2![]() ,
,
∴CE2+BE2=5+20=25,
∵BC2=52=25,
∴BE2+CE2=BC2,
∴∠BEC=90°,
∴△BEC是直角三角形.
(2)四边形EFPH为矩形,
∵矩形ABCD,
∴AD=BC,AD∥BC,
∵DE=BP,
∴四边形DEBP是平行四边形,
∴BE∥DP,
∵AD=BC,AD∥BC,DE=BP,
∴AE=CP,
∴四边形AECP是平行四边形,
∴AP∥CE,
∴四边形EFPH是平行四边形,
∵∠BEC=90°,
∴平行四边形EFPH是矩形.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案【题目】某土产公司组织20辆汽车装运甲、乙、丙三种土特产共120吨去外地销售按计划20辆车都要装运,每辆汽车只能装运同一种土特产,且必须装满,根据下表提供的信息,解答以下问题
土特产种类 | 甲 | 乙 | 丙 |
每辆汽车运载量(吨) | 8 | 6 | 5 |
每吨土特产获利(百元) | 12 | 16 | 10 |
(1)设装运甲种土特产的车辆数为x,装运乙种土特产的车辆数为y,求y与x之间的函数关系式;
(2)如果装运每种土特产的车辆都不少于3辆,那么车辆的安排方案有几种?并写出每种安排方案;
(3)若要使此次销售获利最大,应采用(2)中哪种安排方案?并求出最大利润的值