题目内容
已知:如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=4
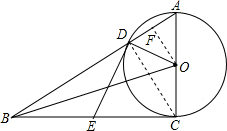
,以AC为直径的⊙ O交AB于点D,点E是BC的中点,连接OD,OB,DE.
O交AB于点D,点E是BC的中点,连接OD,OB,DE.
(1)求证:OD⊥DE;
(2)求sin∠ABO的值.
| 3 |
 O交AB于点D,点E是BC的中点,连接OD,OB,DE.
O交AB于点D,点E是BC的中点,连接OD,OB,DE.(1)求证:OD⊥DE;
(2)求sin∠ABO的值.
(1)证明:连接CD,∵AC是直径,∴∠ADC=∠BDC=90°,(2分)
∵E是BC的中点,
∴DE=BE=EC.(3分)
∵OA=OD,DE=BE,
∴∠ADO=∠A,∠DBE=∠BDE.(4分)
∵∠DBE+∠A=90°,
∴∠BDE+∠ADO=90°,(5分)
∴∠EDO=90°,
∴OD⊥DE.(6分)
(2)过O作OF⊥AD;(7分)
∵在Rt△ABC中,tanA=
=
,
∴∠A=60°,∴△AOD是边长为2的等边三角形,
∴OF=
.(8分)
在Rt△BOC中,BO=
=2
,(9分)
∴sin∠ABO=
=
=
.(10分)
∵E是BC的中点,
∴DE=BE=EC.(3分)
∵OA=OD,DE=BE,
∴∠ADO=∠A,∠DBE=∠BDE.(4分)
∵∠DBE+∠A=90°,
∴∠BDE+∠ADO=90°,(5分)
∴∠EDO=90°,
∴OD⊥DE.(6分)
(2)过O作OF⊥AD;(7分)
∵在Rt△ABC中,tanA=
| BC |
| AC |
| 3 |
∴∠A=60°,∴△AOD是边长为2的等边三角形,
∴OF=
| 3 |
在Rt△BOC中,BO=
| 4+48 |
| 13 |
∴sin∠ABO=
| OF |
| OB |
| ||
2
|
| ||
| 26 |


练习册系列答案
相关题目



 点E.
点E.



