题目内容
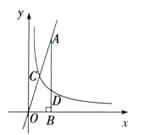
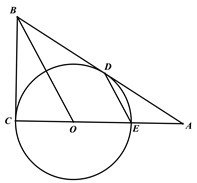
【题目】如图,在![]() ,O是AC上的一点,
,O是AC上的一点, ![]() 与BC,AB分别切于点C,D, 与AC相交于点E,连接BO.
与BC,AB分别切于点C,D, 与AC相交于点E,连接BO.
(1) 求证:CE2=2DE![]() BO;
BO;
(2) 若BC=CE=6,则AE= ,AD= .
【答案】(1)证明见解析;(2)2,4.
【解析】整体分析:
(1)连接CD交![]() ,用对应线段成比例解题;(2)连接OD,设AE=x,由
,用对应线段成比例解题;(2)连接OD,设AE=x,由![]() ,得AB=2(x+3), 在Rt
,得AB=2(x+3), 在Rt ![]() ,由勾股定理求x,即可求解.
,由勾股定理求x,即可求解.
⑴证明:连接CD交![]()
∴BC与![]() O相切于C,
O相切于C, ![]()
![]() EC是
EC是![]() O的直径,
O的直径, ![]() ,
,![]()
![]() BC,BD分别与
BC,BD分别与![]() O相切于C,D,
O相切于C,D, ![]() BO垂直平分CD,
BO垂直平分CD,
从而在Rt![]() 得
得![]()
故![]() ,得
,得![]() ,CE
,CE ![]() ,
,
又![]() CE,
CE, ![]()
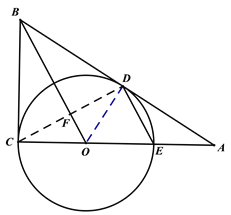
⑵解:连接OD,
![]() BC=CE=6,OD=OE=OC=3,
BC=CE=6,OD=OE=OC=3,
设AE=x,则AO=x+3,AC=x+6.
由![]() ,得AB=2(x+3),
,得AB=2(x+3),
在Rt![]() 由勾股定理得:
由勾股定理得: ![]() ,
,
解得x=2. ![]() .
.
从而在Rt![]() 由勾股定理解得AD=4.
由勾股定理解得AD=4.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
【题目】某校举办“红歌伴我成长”歌咏比赛活动,参赛同学的成绩分别绘制成频数分布表和频数分布直方图(均不完整)如图:
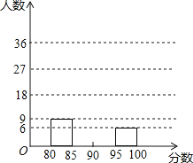
分数段 | 频数 | 频率 |
80≤x<85 | 9 | 0.15 |
85≤x<90 | m | 0.45 |
90≤x<95 | ■ | ■ |
95≤x<100 | 6 | n |
(1)求m,n的值分别是多少;
(2)请在图中补全频数分布直方图;
(3)比赛成绩的中位数落在哪个分数段?