题目内容
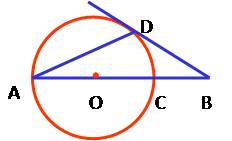
如图,两个等圆⊙O和⊙O¢的两条切线OA、OB,A、B是切点,则∠AOB等于( )
A. 30° B. 45° C. 60° D.90°

A. 30° B. 45° C. 60° D.90°

C
连接OO′和O′A,

根据切线的性质,得O′A⊥OA,根据题意得OO′=2O′A,
则∠AOO′=30°,
再根据切线长定理得∠AOB=2∠AOO′=60°.故选C

根据切线的性质,得O′A⊥OA,根据题意得OO′=2O′A,
则∠AOO′=30°,
再根据切线长定理得∠AOB=2∠AOO′=60°.故选C

练习册系列答案
相关题目
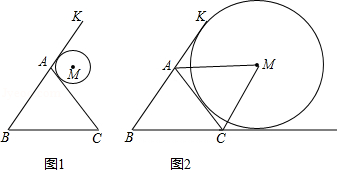
 的边长为
的边长为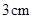 ,边长为
,边长为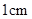 的正
的正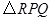 的顶点
的顶点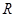 与点
与点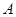 重合,点
重合,点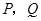 分别在
分别在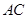 ,
,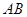 上,将
上,将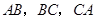 顺时针连续翻转(如图所示),直至点
顺时针连续翻转(如图所示),直至点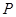 第一次回到原来的位置,则点
第一次回到原来的位置,则点 (结果保留
(结果保留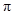 )
)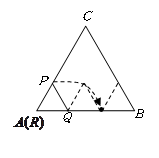
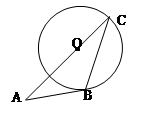
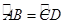 ,则在① AB="CD" ②AC=BD ③
,则在① AB="CD" ②AC=BD ③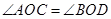 ④
④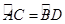 中,正确的个数是( )
中,正确的个数是( )