题目内容
如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限,OA和AB的长是方程 两根,且OA<AB.
两根,且OA<AB.(1)求直线AB的解析式;
(2)将△AOB沿垂直于x轴的线段CD折叠(点C在x轴上,且不与点B重合,点D在线段AB上),使点B落在x轴上,对应点为E,是否存在这样的点C,使得△AED为直角三角形?若存在,求出点C的坐标;若不存在,请说明理由.

【答案】分析:(1)由OA和AB的长是方程x2-3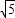 +10=0的两根,且OA<AB,解此方程即可求得OA与AB的长,然后由勾股定理求得OB的长,则可求得点B的坐标;然后作AF⊥x轴于F,由直角三角形的性质,即可求得AF的长,继而由勾股定理求得OF的长,即可求点A的坐标,然后由待定系数法求得直线AB的解析式;
+10=0的两根,且OA<AB,解此方程即可求得OA与AB的长,然后由勾股定理求得OB的长,则可求得点B的坐标;然后作AF⊥x轴于F,由直角三角形的性质,即可求得AF的长,继而由勾股定理求得OF的长,即可求点A的坐标,然后由待定系数法求得直线AB的解析式;
(2)分别从ⅰ)当Rt△AED以点A为直角顶点时,点E与原点O重合与ⅱ)当Rt△AED以点E为直角顶点时去分析求解即可求得答案.
解答:解:(1)∵x2-3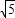 +10=0,
+10=0,
即(x-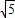 )(x-2
)(x-2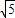 )=0,
)=0,
∴x1=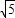 ,x2=2
,x2=2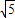 ,
,
∵OA和AB的长是方程x2-3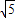 +10=0的两根,且OA<AB,
+10=0的两根,且OA<AB,
∴OA=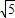 ,AB=2
,AB=2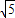 ,
,
∵∠BAO=90°,
∴OB=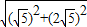 =5,
=5,
作AF⊥x轴于F,如图①:
则AF=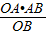 =
= =2,
=2,
∴OF=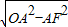 =
=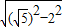 =1,
=1,
∴A(1,2),B(5,0),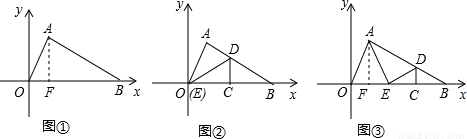
设直线AB的解析式为y=kx+b,
则有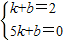 ,
,
解得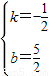 ,
,
∴直线AB的解析式为:y=- x+
x+ ;
;
(2)存在.
分两种情况讨论:
ⅰ)当Rt△AED以点A为直角顶点时,点E与原点O重合,如图②.
∵OC=BC= OB=
OB= ,
,
∴C1( ,0);
,0);
ⅱ)当Rt△AED以点E为直角顶点时,如图③,过点A作AF⊥x轴于F.
则OF=1.
∵∠AED=90°,
∴∠AEO+∠DEC=90°.
∵∠DEC=∠DBC,
∴∠AEO+∠DBC=90°.
又∵∠AOE+∠DBC=90°,
∴∠AOE=∠AEO.
∴△AOE是等腰三角形,
∴OE=2OF=2,
∴BE=3.
∴EC= ,
,
∴OC=OE+EC=2+ =
= .
.
∴C2( ,0).
,0).
综上所述,存在这样的点C,使得△AED为直角三角形,点C的坐标为:C1( ,0)和C2(
,0)和C2( ,0).
,0).
点评:此题考查了待定系数法求一次函数的解析式、直角三角形的性质、等腰三角形的判定与性质以及一元二次方程的解法.此题难度较大,注意掌握方程思想、分类讨论思想与数形结合思想的应用.
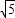 +10=0的两根,且OA<AB,解此方程即可求得OA与AB的长,然后由勾股定理求得OB的长,则可求得点B的坐标;然后作AF⊥x轴于F,由直角三角形的性质,即可求得AF的长,继而由勾股定理求得OF的长,即可求点A的坐标,然后由待定系数法求得直线AB的解析式;
+10=0的两根,且OA<AB,解此方程即可求得OA与AB的长,然后由勾股定理求得OB的长,则可求得点B的坐标;然后作AF⊥x轴于F,由直角三角形的性质,即可求得AF的长,继而由勾股定理求得OF的长,即可求点A的坐标,然后由待定系数法求得直线AB的解析式;(2)分别从ⅰ)当Rt△AED以点A为直角顶点时,点E与原点O重合与ⅱ)当Rt△AED以点E为直角顶点时去分析求解即可求得答案.
解答:解:(1)∵x2-3
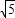 +10=0,
+10=0,即(x-
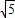 )(x-2
)(x-2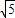 )=0,
)=0,∴x1=
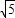 ,x2=2
,x2=2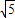 ,
,∵OA和AB的长是方程x2-3
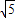 +10=0的两根,且OA<AB,
+10=0的两根,且OA<AB,∴OA=
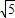 ,AB=2
,AB=2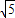 ,
,∵∠BAO=90°,
∴OB=
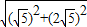 =5,
=5,作AF⊥x轴于F,如图①:
则AF=
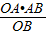 =
= =2,
=2,∴OF=
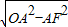 =
=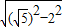 =1,
=1,∴A(1,2),B(5,0),

设直线AB的解析式为y=kx+b,
则有
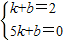 ,
,解得
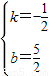 ,
,∴直线AB的解析式为:y=-
 x+
x+ ;
;(2)存在.
分两种情况讨论:
ⅰ)当Rt△AED以点A为直角顶点时,点E与原点O重合,如图②.
∵OC=BC=
 OB=
OB= ,
,∴C1(
 ,0);
,0);ⅱ)当Rt△AED以点E为直角顶点时,如图③,过点A作AF⊥x轴于F.
则OF=1.
∵∠AED=90°,
∴∠AEO+∠DEC=90°.
∵∠DEC=∠DBC,
∴∠AEO+∠DBC=90°.
又∵∠AOE+∠DBC=90°,
∴∠AOE=∠AEO.
∴△AOE是等腰三角形,
∴OE=2OF=2,
∴BE=3.
∴EC=
 ,
,∴OC=OE+EC=2+
 =
= .
.∴C2(
 ,0).
,0).综上所述,存在这样的点C,使得△AED为直角三角形,点C的坐标为:C1(
 ,0)和C2(
,0)和C2( ,0).
,0).点评:此题考查了待定系数法求一次函数的解析式、直角三角形的性质、等腰三角形的判定与性质以及一元二次方程的解法.此题难度较大,注意掌握方程思想、分类讨论思想与数形结合思想的应用.

练习册系列答案
相关题目
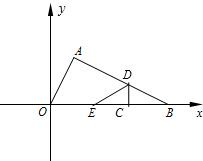 如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限.OA和AB的长是方程
如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限.OA和AB的长是方程 如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限,OA和AB的长是方程
如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限,OA和AB的长是方程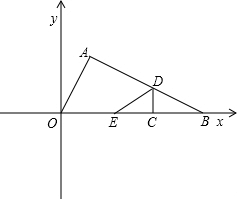 如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限,OA和AB的长是方程
如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限,OA和AB的长是方程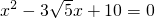 两根,且OA<AB.
两根,且OA<AB.