题目内容
已知正方形ABCD的边长为4cm,有一动点P以1cm/s的速度沿A-B-C-D的路径运动,设P点运动的时间为x(s)(0<x<12),△ADP的面积为ycm2.(1)求y与x的函数关系式;
(2)在给定的平面直角坐标系中画出上述函数关系的图象.
(3)点P运动多长时间时,△ADP是等腰三角形(只写结果).
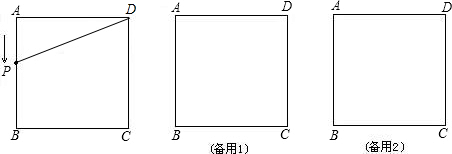
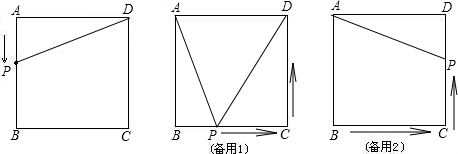
分析:(1)求出AP的长(含x),利用三角形面积公式解答;(2)根据解析式为一次函数或常函数,描出两点即可去确定一条线段,作出三条即可;(3)分点P在B点时,点P在BC中点时点P在C点时三种情况讨论.
解答:解:(1)分三种情况(P在AB、BC、CD上):①因为y=
AD•AP=
×4x,所以y=2x(0<x<4);
②当点P在BC上运动时,三角形APD的底AD和高AB不变,故面积为y=
×4×4=8(4≤x≤8);
③当点P在CD上时,三角形的面积为y=
(4×3-x)×4=-2x+24(8<x<12).
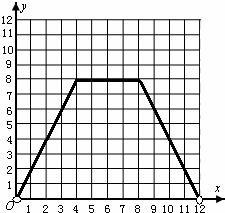
(2)图象如下图:(注意:不包括端点0和12)
(3)点P在B点时,AD=AB,为等腰三角形,x=4÷1=4秒;
点P在BC中点时,AP=DP,为等腰三角形,x=(4+2)÷1=6秒;
点P在C点时,AD=CD,为等腰三角形,x=(4+4)÷1=8秒;
点P运动4或6或8秒时,△ADP是等腰三角形.
| 1 |
| 2 |
| 1 |
| 2 |
②当点P在BC上运动时,三角形APD的底AD和高AB不变,故面积为y=
| 1 |
| 2 |
③当点P在CD上时,三角形的面积为y=
| 1 |
| 2 |

(2)图象如下图:(注意:不包括端点0和12)

(3)点P在B点时,AD=AB,为等腰三角形,x=4÷1=4秒;
点P在BC中点时,AP=DP,为等腰三角形,x=(4+2)÷1=6秒;
点P在C点时,AD=CD,为等腰三角形,x=(4+4)÷1=8秒;
点P运动4或6或8秒时,△ADP是等腰三角形.
点评:此题是一道动点问题,解答时要结合图形,找到构成等腰三角形的关键点,利用三角形的面积公式求出解析式,再进一步解答.

练习册系列答案
相关题目
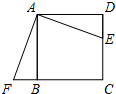 如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为
如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为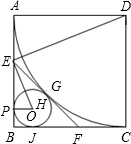 合),过点E作弧AC的切线,交BC于点F,G为切点,⊙O是△EBF的内切圆,分别切EB、BF、FE于点P、J、H
合),过点E作弧AC的切线,交BC于点F,G为切点,⊙O是△EBF的内切圆,分别切EB、BF、FE于点P、J、H (2011•同安区质检)如图,已知正方形ABCD的边长是2,E是AB的中点,延长BC到点F使CF=AE.
(2011•同安区质检)如图,已知正方形ABCD的边长是2,E是AB的中点,延长BC到点F使CF=AE. (2012•香洲区一模)如图,已知正方形ABCD的边长为28,动点P从A开始在线段AD上以每秒3个单位长度的速度向点D运动(点P到达点D时终止运动),动直线EF从AD开始以每秒1个单位长度的速度向下平行移动(即EF∥AD),并且分别与DC、AC交于E、F两点,连接FP,设动点P与动直线EF同时出发,运动时间为t 秒.
(2012•香洲区一模)如图,已知正方形ABCD的边长为28,动点P从A开始在线段AD上以每秒3个单位长度的速度向点D运动(点P到达点D时终止运动),动直线EF从AD开始以每秒1个单位长度的速度向下平行移动(即EF∥AD),并且分别与DC、AC交于E、F两点,连接FP,设动点P与动直线EF同时出发,运动时间为t 秒. 如图,已知正方形ABCD的边长为8cm,点E、F分别在边BC、CD上,∠EAF=45°.当EF=8cm时,△AEF的面积是
如图,已知正方形ABCD的边长为8cm,点E、F分别在边BC、CD上,∠EAF=45°.当EF=8cm时,△AEF的面积是