题目内容
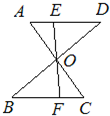3、如图，已知AC和BD相交于O点，AD∥BC，AD=BC，过O任作一条直线分别交AD，BC于点E，F，则下列结论：①OA=OC ②OE=OF ③AE=CF ④OB=OD，其中成立的个数是（ ）分析：由AD∥BC可以推出∠A=∠C，∠B=∠D，又∵AD=BC，由此可以得到△ADO≌△CBO，根据全等三角形的性质得到OA=OC，OB=OD再加上∠AOE=∠COF可以证明△AOE≌△COF，根据全等三角形的性质即可得到OE=OF，AE=CF．
解答：证明：∵AD∥BC，
∴∠A=∠C，∠B=∠D，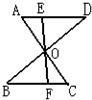
又∵AD=BC，
∴△ADO≌△CBO，
∴OA=OC，OB=OD，
而∠AOE=∠COF，
∴△AOE≌△COF，
∴OE=OF，AE=CF．
故选D．
∴∠A=∠C，∠B=∠D，
又∵AD=BC，
∴△ADO≌△CBO，
∴OA=OC，OB=OD，
而∠AOE=∠COF，
∴△AOE≌△COF，
∴OE=OF，AE=CF．
故选D．
点评：本题考查了全等三角形的判定与全等的性质；题目的难点在于根据前面得到的条件得到△AOE≌△COF，做题时，要结合已知条件与全等的判定方法对选项逐一验证．
练习册系列答案
相关题目
20、如图，已知AC和BD相交于O，且BO=DO，AO=CO，下列判断正确的是（ ）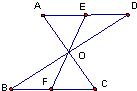
18、如图，已知AC和BD相交于O点，AD∥BC，AD=BC，过O任作一条直线分别交AD，BC于点E、F，则OE
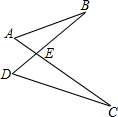如图，已知AC和BD相交于点E，CE•AE=BE•DE，求证：△ABE∽△DCE．
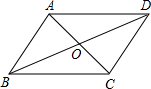如图，已知AC和BD相交于O，且BO=DO，AO=CO．求证：△AOB≌△COD．