题目内容
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点A,将点A向左平移3个单位长度,得到点B,点B在抛物线上.
轴交于点A,将点A向左平移3个单位长度,得到点B,点B在抛物线上.
(1)求点B的坐标(用含m的式子表示);
(2)求抛物线的对称轴;
(3)已知点P(-1,-m),Q(-3,1).若抛物线与线段PQ恰有一个公共点,结合函数图象,求m的取值范围.
【答案】(1)B(-3,-m);(2)x=![]() ;(3)-1≤m<0
;(3)-1≤m<0
【解析】
(1)根据抛物线![]() 与y轴交于点A,将点A向左平移3个单位长度,得到点B,可以先求得点A的坐标,再根据平移的性质得到点B的坐标;
与y轴交于点A,将点A向左平移3个单位长度,得到点B,可以先求得点A的坐标,再根据平移的性质得到点B的坐标;
(2)根据题目中的点A的坐标和(1)中求得的点B的坐标关于对称轴对称,可以求得该抛物线的对称轴;
(3)根据题意,可以画出相应的函数图象,然后利用分类讨论的方法即可得到m的取值范围.
解:(1)依题意得:A(0,-m)
∴B(-3,-m)
(2)∵点A,B关于抛物线的对称轴对称,
∴抛物线的对称轴为x=![]() ;
;
(3)当m>0时,点A(0,-m)在y轴负半轴,
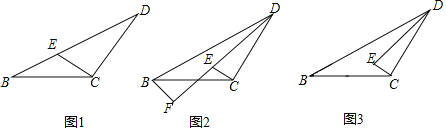
此时,点P,Q位于抛物线内部(如图).
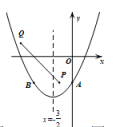
所以,抛物线与线段PQ无交点.
当m<0时,点A(0,-m)在y轴正半轴,
当AQ与x轴平行,即A(0,1)时(如图2),
抛物线与线段PQ恰有一个交点Q(-3,1).
此时,m=-1.
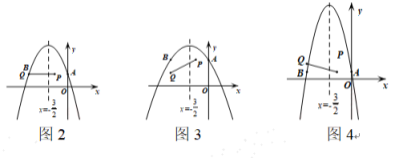
当m>-1时(如图3),结合图象,抛物线与线段PQ无交点.
当-1<m<0时(如图4),结合图象,抛物线与线段PQ恰有一个交点.
综上,m的取值范围是-1≤m<0

【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
①ac<0;
②当x>1时,y的值随x值的增大而减小.
③3是方程ax2+(b﹣1)x+c=0的一个根;
④当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的结论是 .
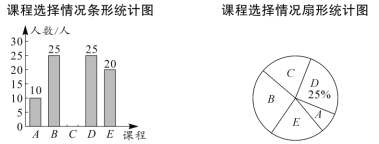
【题目】为了坚持以人民为中心的发展思想,以不断改善民生为发展的根本目的,某机构随机对某小区部分居民进行了关于“社区服务工作满意度”的调查,并根据调查结果绘制成如下不完整的统计图表,根据图标信息,解答下列问题:
满意度 | 人数 | 所占百分比 |
非常满意 | 12 |
|
满意 | 54 |
|
比较满意 |
|
|
不满意 | 6 |
|
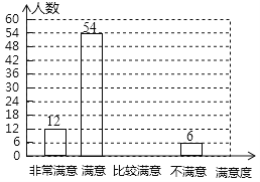
(1)本次调查的总人数为_______.
(2)请补全条形统计图;
(3)据统计,该社区服务站平均每天接待居民约1000名,若将“非常满意”和“消意”作为居民对社区服务站服务工作的肯定,请你估计该社区服务站服务工作平均每天得到多少名居民的肯定.