题目内容
【题目】如图,在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E,若AB=6,求线段DE的长.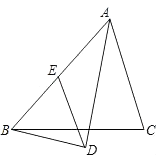
【答案】解:∵AD平分∠BAC,DE∥AC,
∴∠EAD=∠CAD,∠EDA=∠CAD,
∴∠EAD=∠EDA,
∵BD⊥AD,
∴∠EBD+∠EAD=∠BDE+∠EDA
∴∠EBD=∠BDE,
∴DE=BE,
∴DE= ![]() AB=
AB= ![]() ×6=3.
×6=3.
【解析】根据角平分线及平行线的性质得出∠EAD=∠EDA,根据垂直的定义及三角形的内角和得出∠EBD=∠BDE,进而得出DE=BE,根据直角三角形斜边上的中线等于斜边的一半得出答案。
【考点精析】解答此题的关键在于理解角的平分线的相关知识,掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线,以及对平行线的性质的理解,了解两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.

练习册系列答案
相关题目