题目内容
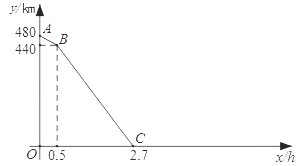
【题目】如图1,某物流公司恰好位于连接A,B两地的一条公路旁的C处.某一天,该公司同时派出甲.乙两辆货车以各自的速度匀速行驶.其中,甲车从公司出发直达B地;乙车从公司出发开往A地,并在A地用1h配货,然后掉头按原速度开往B地.图2是甲.乙两车之间的距离S(km)与他们出发后的时间x(h)之间函数关系的部分图象.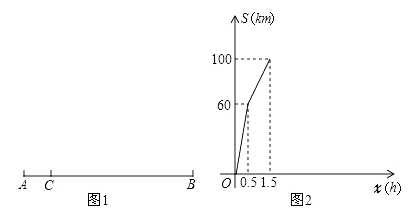
(1)由图象可知,甲车速度为km/h;乙车速度为km/h.
(2)已知最终乙车比甲车早到B地0.5h,求甲车出发1.5h后直至到达B地的过程中,S与x的函数关系式及x的取值范围,并在图2中补全函数图象.
【答案】
(1)40,80
(2)设从1.5小时后两车相遇的时间为t小时,
由题意得,80t-40t=100,
解得t=2.5,
1.5+2.5=4,
此过程中,S=40(x-1.5)+100-80(x-1.5)=-40x+160(1.5≤x≤4),
设甲车到达B地的时间为m,
由题意得,80(m-0.5)-100=40m,
解得m=3.5,
3.5+1.5=5小时,
5-0.5=4.5小时,
乙车到达B地前,S=80(x-4)-40(x-4)=40x-160(4<x≤4.5),
乙车到达B地后,S=40(5-x)=-40x+200(4.5<x≤5),
综上所述,S= 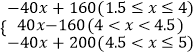
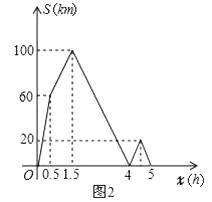
【解析】(1)解:∵乙在A地用1h配货,
∴0.5小时~1.5小时为甲独自行驶,
∴甲的速度=(100-60)÷(1.5-0.5)=40km/h,
乙的速度为:60÷0.5-40=80km/h

【题目】为了解某县2016年初中毕业生的实验考查成绩等级的分布情况,随机抽取了该县若干名学生的实验考查成绩进行统计分析,并根据抽取的成绩绘制了如下的统计图表:
成绩等级 | A | B | C | D |
人数 | 60 | x | y | 10 |
百分比 | 30% | 50% | 15% | m |
请根据以上统计图表提供的信息,解答下列问题:
(1)本次抽查的学生有 名;
(2)表中x,y和m所表示的数分别为:x= ,y= ,m= ;
(3)请补全条形统计图;
(4)根据抽样调查结果,请你估计2016年该县5400名初中毕业生实验考查成绩为D类的学生人数.