题目内容
【题目】如图，点A、B、C在一条直线上，
，
均为等边三角形，连接AE、CD.AE分别交CD、BD于点M．P.CD交BE于点Q．
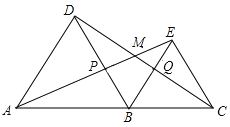
求证：（1）
；
（2）连接MB，MB平分
吗？并说明理由．
【答案】（1）见解析；（2）见解析.
【解析】
（1）根据等边三角形的选择证明得出：△ABE≌ODBC即可
（2）连接MB,根据垂直定理即可证明∠l=∠2,再根据全等三角形的性质可得BI= BJ.即可证明MB平分LAMC.
(1) 
△ABD, △BCE均为等边三角形，
AB= DB，EB=CB，∠ABD=∠C BE= 60°
∠ABD+∠DBE=∠CBE+∠DBE即∠ABE=∠DBC
△ABE≌ODBC
AE= DC.
(2)
连接MB，MB平分∠AMC,
理由是:作BI⊥AE于点I, BJ⊥DC于点J,则∠AIB=∠DJB=90°.
由(1)知，△ABE≌ODBC，AB= DB
∠l=∠2,
△ABI≌△DBJ
BI= BJ.
MB平分∠AMC.
练习册系列答案
阅读快车系列答案
相关题目
