Question

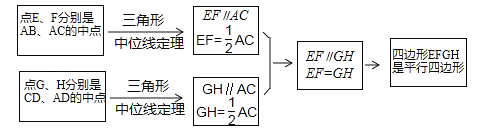
【题目】如图1和图2，∠ACB=90°，AC=BC，BD⊥DE，AE⊥DE，足分别为D、E．

（1）图1中，证明：△ACE≌△CBD；

（2）图2中，若AE=2，BD=4，计算DE的长．

Answer 1

【答案】（1）证明见解析；（2）2.

【解析】试题分析：（1）如图1，根据垂直的定义和同角的余角相等得到∠E=∠D=90°，∠1=∠2，则结合已知条件AC=BC由AAS证得：△ACE≌△CBD；

（2）如图2，同（1），证得△ACE≌△CBD，则根据全等三角形的对应边相等推知：CE=BD=4，AE=CD=2，故DE=CE-CD=4-2=2．

试题解析：（1）证明：如图1，

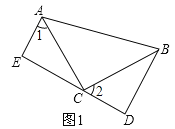
∵BD⊥DE，AE⊥DE，

∴∠E=∠D=90°．

又∵∠ACB=90°，

∴∠1=∠2，

∴在△ACE与△CBD中，

∴△ACE≌△CBD（AAS）；

（2）如图2，

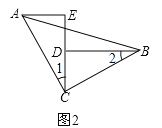
同（1），证得△ACE≌△CBD，则

∴CE=BD=4，AE=CD=2，

∴DE=CE-CD=4-2=2．