Question

【题目】在△ABC中，AB＝AC，过点A作AD⊥AC交射线CB于点D，若△ABD是等腰三角形，则∠C的大小为_____度．

Answer 1

【答案】30或60．

【解析】

分两种情况：△ABD是锐角三角形和钝角三角形来解答。根据等腰三角形的性质得到底角相等，再利用三角形的内角和即可得到结论．

解：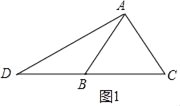

如图1，∵AB＝AC，

∴∠ABC＝∠C，

∵△ABD是等腰三角形，

∴AB＝BD，

∴∠D＝∠DAB，

∵∠ABC＝∠C＝∠D+∠DAB＝2∠D，

∵∠DAC＝90°，

∴∠D+∠C＝∠D +2∠D＝3∠D =90°，

∴∠D＝30°，

∴∠C＝60°；

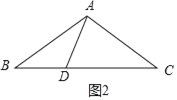
如图2，∵AB＝AC，

∴∠ABC＝∠C，

∵△ABD是等腰三角形，

∴AD＝BD，

∴∠B＝∠DAB，

∵∠ADC＝∠B+∠BAD＝2∠B＝2∠C，

∵∠DAC＝90°，

∴∠ADC+∠C＝90°，

∴∠C＝30°，

故答案为：30或60．