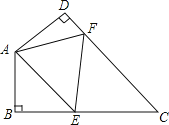
ЬтФПФкШн
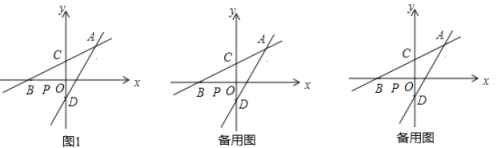
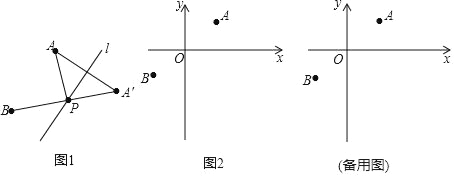
ЁОЬтФПЁПЃЈЖЈвхЃЉШчЭМ1ЃЌAЃЌBЮЊжБЯпlЭЌВрЕФСНЕуЃЌЙ§ЕуAзїжБЯп1ЕФЖдГЦЕуAЁфЃЌСЌНгAЁфBНЛжБЯпlгкЕуPЃЌСЌНгAPЃЌдђГЦЕуPЮЊЕуAЃЌBЙигкжБЯпlЕФЁАЕШНЧЕуЁБЃЎ
ЃЈдЫгУЃЉШчЭМ2ЃЌдкЦНУцжБзјБъЯЕxOyжаЃЌвбжЊAЃЈ2ЃЌ![]() ЃЉЃЌBЃЈЉ2ЃЌЉ
ЃЉЃЌBЃЈЉ2ЃЌЉ![]() ЃЉСНЕуЃЎ
ЃЉСНЕуЃЎ
ЃЈ1ЃЉCЃЈ4ЃЌ![]() ЃЉЃЌDЃЈ4ЃЌ
ЃЉЃЌDЃЈ4ЃЌ![]() ЃЉЃЌEЃЈ4ЃЌ
ЃЉЃЌEЃЈ4ЃЌ![]() ЃЉШ§ЕужаЃЌЕуЁЁ ЁЁЪЧЕуAЃЌBЙигкжБЯпx=4ЕФЕШНЧЕуЃЛ
ЃЉШ§ЕужаЃЌЕуЁЁ ЁЁЪЧЕуAЃЌBЙигкжБЯпx=4ЕФЕШНЧЕуЃЛ
ЃЈ2ЃЉШєжБЯпlДЙжБгкxжсЃЌЕуPЃЈmЃЌnЃЉЪЧЕуAЃЌBЙигкжБЯпlЕФЕШНЧЕуЃЌЦфжаmЃО2ЃЌЁЯAPB=ІСЃЌЧѓжЄЃКtan![]() =
=![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШєЕуPЪЧЕуAЃЌBЙигкжБЯпy=ax+bЃЈaЁй0ЃЉЕФЕШНЧЕуЃЌЧвЕуPЮЛгкжБЯпABЕФгвЯТЗНЃЌЕБЁЯAPB=60ЁуЪБЃЌЧѓbЕФШЁжЕЗЖЮЇЃЈжБНгаДГіНсЙћЃЉЃЎ
ЁОД№АИЁПЃЈ1ЃЉCЃЈ2ЃЉ![]() ЃЈ3ЃЉbЃМЉ
ЃЈ3ЃЉbЃМЉ![]() ЧвbЁйЉ2
ЧвbЁйЉ2![]() ЛђbЃО
ЛђbЃО![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЯШЧѓГіBЙигкжБЯпx=4ЕФЖдГЦЕуBЁфЕФзјБъЃЌИљОнAЁЂBЁфЕФзјБъПЩЕУжБЯпABЁфЕФНтЮіЪНЃЌАбx=4ДњШыЧѓГіPЕуЕФзнзјБъМДПЩЕУД№АИЃЛЃЈ2ЃЉШчЭМЃКЙ§ЕуAзїжБЯпlЕФЖдГЦЕуAЁфЃЌСЌAЁфBЁфЃЌНЛжБЯпlгкЕуPЃЌзїBHЁЭlгкЕуHЃЌИљОнЖдГЦадПЩжЊЁЯAPG=AЁфPGЃЌгЩЁЯAGP=ЁЯBHP=90ЁуПЩжЄУїЁїAGPЁзЁїBHPЃЌИљОнЯрЫЦШ§НЧаЮЖдгІБпГЩБШР§ПЩЕУm=![]()
ИљОнЭтНЧаджЪПЩжЊЁЯA=ЁЯAЁф=![]() ЃЌдкRtЁїAGPжаЃЌИљОне§ЧаЖЈвхМДПЩЕУНсТлЃЛЃЈ3ЃЉЕБЕуPЮЛгкжБЯпABЕФгвЯТЗНЃЌЁЯAPB=60ЁуЪБЃЌЕуPдквдABЮЊЯвЃЌЫљЖддВжмЮЊ60ЁуЃЌЧвдВаФдкABЯТЗНЃЌШєжБЯпy=ax+bЃЈaЁй0ЃЉгыдВЯрНЛЃЌЩшдВгыжБЯпy=ax+bЃЈaЁй0ЃЉЕФСэвЛИіНЛЕуЮЊQ
ЃЌдкRtЁїAGPжаЃЌИљОне§ЧаЖЈвхМДПЩЕУНсТлЃЛЃЈ3ЃЉЕБЕуPЮЛгкжБЯпABЕФгвЯТЗНЃЌЁЯAPB=60ЁуЪБЃЌЕуPдквдABЮЊЯвЃЌЫљЖддВжмЮЊ60ЁуЃЌЧвдВаФдкABЯТЗНЃЌШєжБЯпy=ax+bЃЈaЁй0ЃЉгыдВЯрНЛЃЌЩшдВгыжБЯпy=ax+bЃЈaЁй0ЃЉЕФСэвЛИіНЛЕуЮЊQ
ИљОнЖдГЦаджЪПЩжЄУїЁїABQЪЧЕШБпШ§НЧаЮЃЌМДЕуQЮЊЖЈЕуЃЌШєжБЯпy=ax+bЃЈaЁй0ЃЉгыдВЯрЧаЃЌвзЕУPЁЂQжиКЯЃЌЫљвджБЯпy=ax+bЃЈaЁй0ЃЉЙ§ЖЈЕуQЃЌСЌOQЃЌЙ§ЕуAЁЂQЗжБ№зїAMЁЭyжсЃЌQNЁЭyжсЃЌДЙзуЗжБ№ЮЊMЁЂNЃЌПЩжЄУїЁїAMOЁзЁїONQЃЌИљОнЯрЫЦШ§НЧаЮЖдгІБпГЩБШР§ПЩЕУONЁЂNQЕФГЄЃЌМДПЩЕУQЕузјБъЃЌИљОнAЁЂBЁЂQЕФзјБъПЩЧѓГіжБЯпAQЁЂBQЕФНтЮіЪНЃЌИљОнPгыAЁЂBжиКЯЪБbЕФжЕЧѓГіbЕФШЁжЕЗЖЮЇМДПЩ.
ЃЈ1ЃЉЕуBЙигкжБЯпx=4ЕФЖдГЦЕуЮЊBЁфЃЈ10ЃЌЉ![]() ЃЉЃЌ
ЃЉЃЌ
ЁржБЯпABЁфНтЮіЪНЮЊЃКy=Љ![]() ЃЌ
ЃЌ
ЕБx=4ЪБЃЌy=![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃКC
ЃЈ2ЃЉШчЭМЃЌЙ§ЕуAзїжБЯпlЕФЖдГЦЕуAЁфЃЌСЌAЁфBЁфЃЌНЛжБЯпlгкЕуP
зїBHЁЭlгкЕуH
ЁпЕуAКЭAЁфЙигкжБЯпlЖдГЦ
ЁрЁЯAPG=ЁЯAЁфPG
ЁпЁЯBPH=ЁЯAЁфPG
ЁрЁЯAPG=ЁЯBPH
ЁпЁЯAGP=ЁЯBHP=90Ёу
ЁрЁїAGPЁзЁїBHP
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
Ёрmn=2![]() ЃЌМДm=
ЃЌМДm=![]() ЃЌ
ЃЌ
ЁпЁЯAPB=ІСЃЌAP=APЁфЃЌ
ЁрЁЯA=ЁЯAЁф=![]() ЃЌ
ЃЌ
дкRtЁїAGPжаЃЌtan![]()
![]()
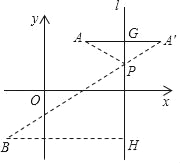
ЃЈ3ЃЉШчЭМЃЌЕБЕуPЮЛгкжБЯпABЕФгвЯТЗНЃЌЁЯAPB=60ЁуЪБЃЌ
ЕуPдквдABЮЊЯвЃЌЫљЖддВжмЮЊ60ЁуЃЌЧвдВаФдкABЯТЗН
ШєжБЯпy=ax+bЃЈaЁй0ЃЉгыдВЯрНЛЃЌЩшдВгыжБЯпy=ax+bЃЈaЁй0ЃЉЕФСэвЛИіНЛЕуЮЊQ
гЩЖдГЦадПЩжЊЃКЁЯAPQ=ЁЯAЁфPQЃЌ
гжЁЯAPB=60Ёу
ЁрЁЯAPQ=ЁЯAЁфPQ=60Ёу
ЁрЁЯABQ=ЁЯAPQ=60ЁуЃЌЁЯAQB=ЁЯAPB=60Ёу
ЁрЁЯBAQ=60Ёу=ЁЯAQB=ЁЯABQ
ЁрЁїABQЪЧЕШБпШ§НЧаЮ
ЁпЯпЖЮABЮЊЖЈЯпЖЮ
ЁрЕуQЮЊЖЈЕу
ШєжБЯпy=ax+bЃЈaЁй0ЃЉгыдВЯрЧаЃЌвзЕУPЁЂQжиКЯ
ЁржБЯпy=ax+bЃЈaЁй0ЃЉЙ§ЖЈЕуQ
СЌOQЃЌЙ§ЕуAЁЂQЗжБ№зїAMЁЭyжсЃЌQNЁЭyжсЃЌДЙзуЗжБ№ЮЊMЁЂN
ЁпAЃЈ2ЃЌ![]() ЃЉЃЌBЃЈЉ2ЃЌЉ
ЃЉЃЌBЃЈЉ2ЃЌЉ![]() ЃЉ
ЃЉ
ЁрOA=OB=![]()
ЁпЁїABQЪЧЕШБпШ§НЧаЮ
ЁрЁЯAOQ=ЁЯBOQ=90ЁуЃЌOQ=![]() ЃЌ
ЃЌ
ЁрЁЯAOM+ЁЯNOD=90Ёу
гжЁпЁЯAOM+ЁЯMAO=90ЁуЃЌЁЯNOQ=ЁЯMAO
ЁпЁЯAMO=ЁЯONQ=90Ёу
ЁрЁїAMOЁзЁїONQ
Ёр![]() ,
,
Ёр![]() ЃЌ
ЃЌ
ЁрON=2![]() ЃЌNQ=3ЃЌЁрQЕузјБъЮЊЃЈ3ЃЌЉ2
ЃЌNQ=3ЃЌЁрQЕузјБъЮЊЃЈ3ЃЌЉ2![]() ЃЉ
ЃЉ
ЩшжБЯпBQНтЮіЪНЮЊy=kx+b
НЋBЁЂQзјБъДњШыЕУ
![]() ЃЌ
ЃЌ
НтЕУ
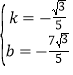 ЃЌ
ЃЌ
ЁржБЯпBQЕФНтЮіЪНЮЊЃКy=Љ![]() ЃЌ
ЃЌ
ЩшжБЯпAQЕФНтЮіЪНЮЊЃКy=mx+nЃЌ
НЋAЁЂQСНЕуДњШы![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
ЁржБЯпAQЕФНтЮіЪНЮЊЃКy=Љ3![]() ЃЌ
ЃЌ
ШєЕуPгыBЕужиКЯЃЌдђжБЯпPQгыжБЯпBQжиКЯЃЌДЫЪБЃЌb=Љ![]() ЃЌ
ЃЌ
ШєЕуPгыЕуAжиКЯЃЌдђжБЯпPQгыжБЯпAQжиКЯЃЌДЫЪБЃЌb=![]() ЃЌ
ЃЌ
гжЁпy=ax+bЃЈaЁй0ЃЉЃЌЧвЕуPЮЛгкABгвЯТЗНЃЌ
ЁрbЃМЉ![]() ЧвbЁйЉ2
ЧвbЁйЉ2![]() ЛђbЃО
ЛђbЃО![]() .
.

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ