题目内容
 如图,在直角坐标平面内,O为原点,点A的坐标为(13,0),点B在第一象限内,BO=5,sin∠BOA=
如图,在直角坐标平面内,O为原点,点A的坐标为(13,0),点B在第一象限内,BO=5,sin∠BOA= .求:
.求:
(1)点B的坐标;
(2)cos∠BAO的值.
 解:(1)如图,过点B作BH⊥OA于H,
解:(1)如图,过点B作BH⊥OA于H,∵OB=5,sin∠BOA=
 ,
,∴BH=3,OH=4,
∴点B的坐标为(4,3),
(2)∵OA=13,
∴AH=9,
∴在Rt△AHB中,AB=3
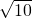
∴cos∠BAO=
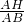 =
= =
=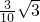
分析:(1)由题意,过点B作BH⊥OA于H,根据BO=5,sin∠BOA=
 ,可得BH=3,OH=4,即可得出;
,可得BH=3,OH=4,即可得出;(2)如图,根据题意,OA=10,可得AH=6,所以,在Rt△AHB中,可得sin∠BAO的值.
点评:本题主要考查了解直角三角形和坐标与图形性质,根据题意,借助辅助线,是解答本题的关键.

练习册系列答案
相关题目
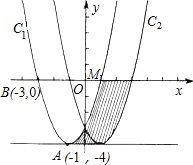 如图,在直角坐标平面xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0)
如图,在直角坐标平面xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0) 如图,在直角坐标平面中,Rt△ABC的斜边AB在x轴上,直角顶点C在y轴的负半轴上,cos∠ABC=
如图,在直角坐标平面中,Rt△ABC的斜边AB在x轴上,直角顶点C在y轴的负半轴上,cos∠ABC=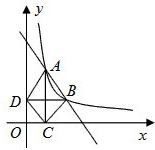 如图,在直角坐标平面内,函数y=
如图,在直角坐标平面内,函数y=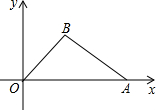 完成下列各题:
完成下列各题: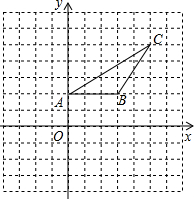 如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点C的坐标为(5,5),要使以A、B、C、D为顶点的四边形是平行四边形,且点D坐标在第一象限,那么点D的坐标是
如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点C的坐标为(5,5),要使以A、B、C、D为顶点的四边形是平行四边形,且点D坐标在第一象限,那么点D的坐标是