题目内容
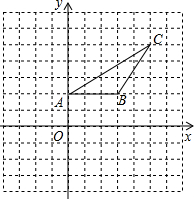如图，在直角坐标平面内的△ABC中，点A的坐标为（0，2），点C的坐标为（5，5），要使以A、B、C、D为顶点的四边形是平行四边形，且点D坐标在第一象限，那么点D的坐标是（2，5）或（8，5）
（2，5）或（8，5）
．分析：根据平行四边形的性质，可知CD∥AB，所以点D的纵坐标是5，再由AB间的距离即可推导出点D的纵坐标．
解答：解：由平行四边形的性质，可知D点的纵坐标一定是5；
又由A点相对于B点横坐标移动了3-0=3，故可得点D横坐标为5-3=2，即顶点D的坐标（2，5）；
再由B点相对于A点横坐标移动了0+3=3，故可得点D横坐标为5+3=8，即顶点D的坐标（8，5）．
故答案为：（2，5）或（8，5）．
又由A点相对于B点横坐标移动了3-0=3，故可得点D横坐标为5-3=2，即顶点D的坐标（2，5）；
再由B点相对于A点横坐标移动了0+3=3，故可得点D横坐标为5+3=8，即顶点D的坐标（8，5）．
故答案为：（2，5）或（8，5）．
点评：本题主要考查了平行四边形的判定和坐标与图形的性质，同时又考查了数形结合思想，题目的条件既有数又有形，解决问题的方法也要既依托数也依托形，体现了数形的紧密结合．
练习册系列答案
相关题目
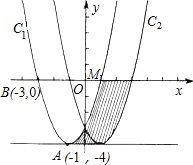如图，在直角坐标平面xOy中，抛物线C1的顶点为A（-1，-4），且过点B（-3，0）
如图，在直角坐标平面中，Rt△ABC的斜边AB在x轴上，直角顶点C在y轴的负半轴上，cos∠ABC=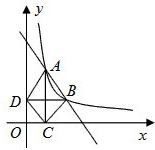
如图，在直角坐标平面内，函数y=
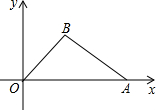完成下列各题：