题目内容
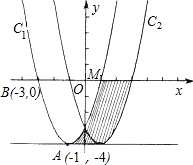 如图,在直角坐标平面xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0)
如图,在直角坐标平面xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0)(1)写出抛物线C1与x轴的另一个交点M的坐标;
(2)将抛物线C1向右平移2个单位得抛物线C2,求抛物线C2的解析式;
(3)写出阴影部分的面积S.
分析:(1)由抛物线C1的顶点为A(-1,-4),故对称轴x=-1,B、M两点关于x=1对称,求得另一坐标.
(2)设抛物线C1的解析式为y=a(x+1)2-4,将B点代入解析式,求a,由抛物线C1向右平移2个单位得抛物线C2,故能得抛物线C2的解析式.
(3)阴影部分可以转换成求平行四边形的面积,即函数图象平移的距离乘以A点纵坐标的绝对值.
(2)设抛物线C1的解析式为y=a(x+1)2-4,将B点代入解析式,求a,由抛物线C1向右平移2个单位得抛物线C2,故能得抛物线C2的解析式.
(3)阴影部分可以转换成求平行四边形的面积,即函数图象平移的距离乘以A点纵坐标的绝对值.
解答:解:(1)由抛物线C1的顶点为A(-1,-4),
故对称轴x=-1,x=
,
解得m=1,
故M(1,0).
(2)设抛物线C1的解析式为y=a(x+1)2-4,
将点B(-3,0)代入得a=1,
∴抛物线的解析式为y=(x+1)2-4,
∵将抛物线C1向右平移2个单位得抛物线C2,
∴抛物线C2的解析式为y=(x-1)2-4.
(3)阴影部分可以转换成求平行四边形的面积,S=2×|yA|=2×4=8.
故对称轴x=-1,x=
| -3+m |
| 2 |
解得m=1,
故M(1,0).
(2)设抛物线C1的解析式为y=a(x+1)2-4,
将点B(-3,0)代入得a=1,
∴抛物线的解析式为y=(x+1)2-4,
∵将抛物线C1向右平移2个单位得抛物线C2,
∴抛物线C2的解析式为y=(x-1)2-4.
(3)阴影部分可以转换成求平行四边形的面积,S=2×|yA|=2×4=8.
点评:本题是二次函数的综合题,涉及知识点有抛物线的对称轴的求法,平移,面积求法等知识点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
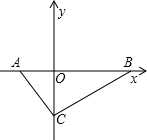 如图,在直角坐标平面中,Rt△ABC的斜边AB在x轴上,直角顶点C在y轴的负半轴上,cos∠ABC=
如图,在直角坐标平面中,Rt△ABC的斜边AB在x轴上,直角顶点C在y轴的负半轴上,cos∠ABC=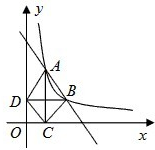 如图,在直角坐标平面内,函数y=
如图,在直角坐标平面内,函数y= 完成下列各题:
完成下列各题: 如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点C的坐标为(5,5),要使以A、B、C、D为顶点的四边形是平行四边形,且点D坐标在第一象限,那么点D的坐标是
如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点C的坐标为(5,5),要使以A、B、C、D为顶点的四边形是平行四边形,且点D坐标在第一象限,那么点D的坐标是