题目内容
 如图,在直角坐标平面中,Rt△ABC的斜边AB在x轴上,直角顶点C在y轴的负半轴上,cos∠ABC=
如图,在直角坐标平面中,Rt△ABC的斜边AB在x轴上,直角顶点C在y轴的负半轴上,cos∠ABC=| 4 | 5 |
(1)求P点坐标;
(2)求AP的长;
(3)在x轴上是否存在点Q,使以A、Q、C、P为顶点的四边形是梯形?若存在,请求出直线PQ的解析式;若不存在,请说明理由.
分析:(1)通过解方程x2-15x+36=0,得OP、OC的长度,即可推出P点的坐标,(2)根据直角三角形的性质,推出Cos∠ABC=
=Cos∠ACO=
,结合已知条件即可推出AP的长度,
(3)首先设出Q点的坐标,分情况讨论,①AP∥CQ,然后根据
=
,即可求出OQ的长度,即可得Q点的坐标,然后根据P和Q点的坐标即可推出直线PQ的解析式,②PQ∥AC,分别求出即可.
| 4 |
| 5 |
| OC |
| AC |
(3)首先设出Q点的坐标,分情况讨论,①AP∥CQ,然后根据
| OA |
| OQ |
| OP |
| OC |
解答:解:(1)∵PO、OC的长是方程x2-15x+36=0的两根,OC>PO,
∴PO=3,OC=12(2分)
∴P(0,-3)(2分)
(2)在Rt△OBC与Rt△AOC中,cos∠ABC=
=cos∠ACO,
∴
=
(1分)
设CO=4K,AC=5K,∴CO=4K=12,K=3
∴AO=3K=9,∴A(-9,0)(2分)
∴AP=
=3
(1分)
(3)设在x轴上存在点Q(x,0)使四边形AQCP是梯形,
①AP∥CQ,∴
=
,
∵OA=9,OP=3,OC=12,
∴OQ=36,则Q(-36,0),
设直线PQ的解析式为y=kx+b,将点P(0,-3),Q(-36,0)代入,得
,
解得:
,
②同理当PQ∥AC,可得PQ的解析式为:y=-
x+3;
∴所求直线PQ的解析式为y=-
x-3或y=-
x+3.
∴PO=3,OC=12(2分)
∴P(0,-3)(2分)
(2)在Rt△OBC与Rt△AOC中,cos∠ABC=
| 4 |
| 5 |
∴
| CO |
| AC |
| 4 |
| 5 |
设CO=4K,AC=5K,∴CO=4K=12,K=3
∴AO=3K=9,∴A(-9,0)(2分)
∴AP=
| 81+9 |
| 10 |
(3)设在x轴上存在点Q(x,0)使四边形AQCP是梯形,
①AP∥CQ,∴
| OA |
| OQ |
| OP |
| OC |
∵OA=9,OP=3,OC=12,
∴OQ=36,则Q(-36,0),
设直线PQ的解析式为y=kx+b,将点P(0,-3),Q(-36,0)代入,得
|
解得:
|
②同理当PQ∥AC,可得PQ的解析式为:y=-
| 4 |
| 3 |
∴所求直线PQ的解析式为y=-
| 1 |
| 12 |
| 4 |
| 3 |
点评:本题主要考查解整式方程、解直角三角形、勾股定理、平行线的相关性质、求一次函数解析式,关键在于确定P点的坐标;根据解直角三角形求得AP的长度;根据平行线的性质,确定OQ的长度,确定Q点的坐标.

练习册系列答案
相关题目
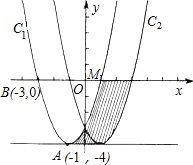 如图,在直角坐标平面xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0)
如图,在直角坐标平面xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0)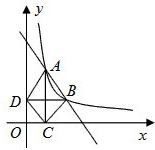 如图,在直角坐标平面内,函数y=
如图,在直角坐标平面内,函数y=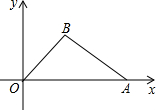 完成下列各题:
完成下列各题: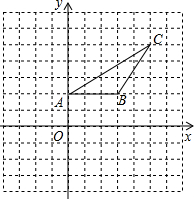 如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点C的坐标为(5,5),要使以A、B、C、D为顶点的四边形是平行四边形,且点D坐标在第一象限,那么点D的坐标是
如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点C的坐标为(5,5),要使以A、B、C、D为顶点的四边形是平行四边形,且点D坐标在第一象限,那么点D的坐标是