题目内容
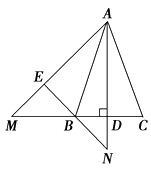
【题目】如图,△ABC中,∠ACB=90°,∠ABC=60°,AB=8cm,D是AB的中点.现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M点.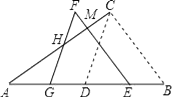
(1)求证:AG=GH;
(2)求四边形GHME的面积.
【答案】
(1)证明:将△BCD沿BA方向平移得到△EFG,
∴△BCD≌△EFG,FG∥CD,EF∥CB,DG=EB=1,
∵∠ACB=90°,D是AB的中点,
∴AD=CD=BD= ![]() AB=
AB= ![]() ×8=4,
×8=4,
∴∠DAC=∠ACD,
∵FG∥CD,
∴∠AFG=∠ACD,
∴∠AHG=∠DAC,
∴AG=GH
(2)解:如图:过C作CN⊥AB于N,

∵∠ABC=60°,∠ACB=90°,
∵BC= ![]() AB=
AB= ![]() ×8=4,
×8=4,
∵∠ABC=60°,CD=BD,
∴△BCD为等边三角形,
∴NB= ![]() BD=2,
BD=2,
∴CN= ![]() ,
,
∵DG=1,AD=4,
∴GH=AG=3,
∴FH=1,you
∵∠A=30°,
∴∠A=30°=∠AHG=∠FHM=30°,
∵FE∥CB,∠ACB=90°,
∴MF= ![]() ,
,
∴HM= ![]() .
.
∴S△EFG=S△BCD= ![]() ×4×2
×4×2 ![]() =4
=4 ![]() ,
,
S△MFH= ![]() ×
× ![]() ×
× ![]() =
= ![]() ,
,
【解析】(1)由点D是直角三角形的斜边AB的中点,得到CD=AD=DB,根据等边对等角,得出∠A=∠ACD,由平移得到FG∥CD,则可得∠AHG=∠ACD,即可得∠AHG=∠A,等角对等边得到AG=GH;(2)四边形GHME是由直角三角形AME减去等腰三角形AGH得到的。

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目