Question

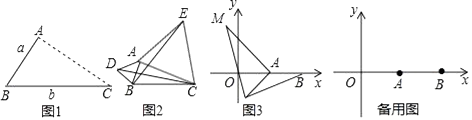
【题目】如图，已知点C为直线y=x上在第一象限内一点，直线y=2x+1交y轴于点A，交x轴于B，将直线AB沿射线OC方向平移 个单位，则平移后直线的解析式为。

Answer 1

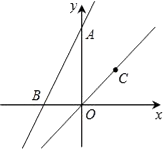
【答案】y=2x
【解析】设点A沿射线OC方向平移 个单位后到达点M，点B沿射线OC方向平移 个单位后到达点N，过点M作ME⊥y轴于点M，过点N作NF⊥x轴于点F，如图所示．

∵直线OC的解析式为y=x，

∴∠COF=∠COA=45°．

∵AM∥OC、BN∥OC，

∴∠NBF=∠COF=45°，∠MAE=∠COA=45°，

∴△AEM和△BFN为等腰直角三角形，且AM=BN= ，

∴BF=NF=AE=EM=1．

当x=0时，y=2x+1=1，

∴点A的坐标为（0，1）；

当y=2x+1=0时，x=﹣ ，

∴点B的坐标为（﹣ ，0）．

∴点M的坐标为（1，2），点N的坐标为（ ，1）．

设直线MN的解析式为y=kx+b，

将M（1，2）、N（ ，1）代入y=kx+b，

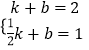，解得： ，

∴直线MN的解析式为y=2x．

故答案为：y=2x．

先画出平移后的图像，设设点A沿射线OC方向平移 个单位后到达点M，点B沿射线OC方向平移个单位后到达点N，过点M作ME⊥y轴于点M，过点N作NF⊥x轴于点F，根据直线OC的解析式为直线y=x及AM∥OC、BN∥OC，可证出∠NBF=∠COF=∠MAE=∠COA=45°，平移的距离为AM=BN= ，利用勾股定理求出BF=NF=AE=EM=1，再求出直线y=2x+1与x轴和y轴的交点坐标，从而得出点M、N的坐标，然后利用待定系数法求出直线MN的函数解析式。