题目内容
【题目】在数学活动课上，老师要求学生在5×5的正方形ABCD网格中（小正方形的边长为1）画直角三角形，要求三个顶点都在格点上，而且三边与AB或AD都不平行．画四种图形，并直接写出其周长（所画图象相似的只算一种）．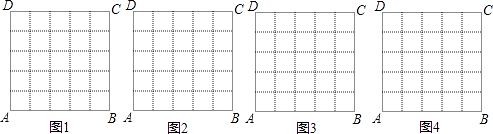 
【答案】解：如图1，三角形的周长=2 
+ 
； 如图2，三角形的周长=4 
+2 ；
如图3，三角形的周长=5 + 
；
如图4，三角形的周长=3 + ．
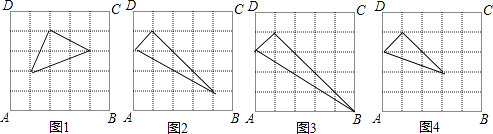
【解析】在图1中画等腰直角三角形；在图2、3、4中画有一条直角边为 
，另一条直角边分别为3 ，4 ，2 的直角三角形，然后计算出四个直角三角形的周长．
【考点精析】通过灵活运用勾股定理的概念，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】某水果基地计划装运甲、乙、丙三种水果到外地销售（每辆汽车规定满载，并且只装一种水果）．如表为装运甲、乙、丙三种水果的重量及利润．
甲 | 乙 | 丙 | |
每辆汽车能装的数量（吨） | 4 | 2 | 3 |
每吨水果可获利润（千元） | 5 | 7 | 4 |
（1）用8辆汽车装运乙、丙两种水果共22吨到A地销售，问装运乙、丙两种水果的汽车各多少辆？
（2）水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售（每种水果不少于一车），假设装运甲水果的汽车为m辆，则装运乙、丙两种水果的汽车各多少辆？（结果用m表示）
（3）在（2）问的基础上，如何安排装运可使水果基地获得最大利润？最大利润是多少？
【题目】张老师要从班级里数学成绩较优秀的甲、乙两位学生中选拔一人参加“全国初中数学联赛” 
为此，他对两位同学进行了辅导，并在辅导期间测验了10次，测验成绩如下表：
第1次 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
甲 | 68 | 80 | 78 | 79 | 78 | 84 | 81 | 83 | 77 | 92 |
乙 | 86 | 80 | 75 | 83 | 79 | 80 | 85 | 80 | 77 | 75 |
利用表中数据，解答下列问题：
填空完成下表：
平均成绩 | 中位数 | 众数 | |
甲 | 80 |
| |
乙 | 80 | 80 |
张老师从测验成绩表中，求得甲的方差
，请你计算乙10次测验成绩的方差．
请你根据上面的信息，运用所学统计知识，帮张老师选拔出参加“全国数学联赛”的人选，并简要说明理由．