Question

【题目】如图，在Rt△ABC中，∠ACB=90°，AC=2 ，以点C为圆心，CB的长为半径画弧，与AB边交于点D，将 绕点D旋转180°后点B与点A恰好重合，则图中阴影部分的面积为

Answer 1

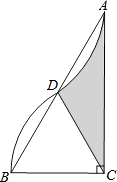
【答案】
【解析】解：由旋转可知AD=BD， ∵∠ACB=90°，AC=2 ，
∴CD=BD，
∵CB=CD，
∴△BCD是等边三角形，
∴∠BCD=∠CBD=60°，
∴BC= AC=2，
∴阴影部分的面积=2 ×2÷2﹣ = ．
所以答案是： ．
【考点精析】利用扇形面积计算公式和旋转的性质对题目进行判断即可得到答案，需要熟知在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）；①旋转后对应的线段长短不变，旋转角度大小不变；②旋转后对应的点到旋转到旋转中心的距离不变；③旋转后物体或图形不变，只是位置变了．