题目内容
【题目】如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．
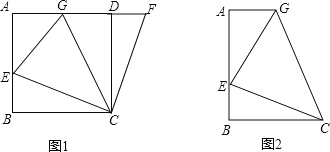
（1）①试说明CE=CF，∠BCE=∠DCF；
②如图1，若点G在AD上，且∠GCE=45°，则GE=GF成立吗？为什么？
（2）运用（1）中积累的经验和知识，完成下题：
如图2，在梯形ABCG中，AG∥BC，BC＞AG，∠B=90°，AB=BC=6，E是AB上 一点，且∠GCE=45°，BE=2，求GE的长．
【答案】（1）成立（2）GE=5
【解析】
试题分析：（1）①根据正方形的性质可得BC=CD，再利用“边角边”证明△BCE和△DCF全等，根据全等三角形对应边相等、对应角相等的单结论；
②根据全等三角形对应角相等可得∠BCE=∠DCF，再求出∠GCF=45°，从而得到∠GCF=∠GCE，再利用“边角边”证明△GCE和△GCF全等，根据全等三角形对应边相等可得EG=GF；
（2）设EG=x，根据（1）的结论表示出AG，再求出AE，然后在Rt△AEG中，利用勾股定理列出方程求解即可．
（1）①证明：在正方形ABCD中，BC=CD，
在△BCE和△DCF中，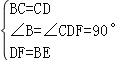
，
∴△BCE≌△DCF（SAS），
∴CE=CF；，∠BCE=∠DCF
②EG=BE+GD．
理由如下：∵△BCE≌△DCF，
∴∠BCE=∠DCF，
∵∠GCE=45°，
∴∠GCF=∠GCD+∠DCF=∠GCD+∠BCE=90°﹣45°=45°，
∴∠GCF=∠GCE，
在△GCE和△GCF中，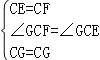
，
∴△GCE≌△GCF（SAS），
∴EG=GF；
（2）设EG=x，
由（1）可知，BE+（6﹣AG）=EG，
即2+（6﹣AG）=x，
∴AG=8﹣x，
又∵AE=AB﹣BE=6﹣2=4，
∴在Rt△AEG中，AE2+AG2=EG2，
即42+（8﹣x）2=x2，
解得x=5，
即GE=5．
