��Ŀ����
����Ŀ����1�������龳����ͼ1����������ABCD�У�E��F��G��H�ֱ�ΪAB��BC��CD��DA���ϵĶ��㣬����EG��HF�ཻ�ڵ�O���ҡ�HOE=��ADC����̽����EG��FH��������ϵ����˵�����ɣ�
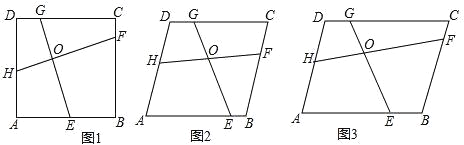
��2����չ���죺��ͼ2��������ABCD�У�E��F��G��H�ֱ�ΪAB��BC��CD��DA���ϵĶ��㣬����EG��HF�ཻ�ڵ�O���ҡ�HOE=��ADC����̽������1����EG��FH��������ϵ�������𣿲�˵�����ɣ�
��3����˼������������2���е�����ABCD��Ϊƽ���ı���ABCD����ͼ3����AB=a��AD=b�������������䣬��![]() �IJ�����ȷ����˵�����ɣ�
�IJ�����ȷ����˵�����ɣ�
���𰸡���1��EG=FH,���ɼ���������2�����������ɼ���������3����ȷ�����ɼ�����.
��������
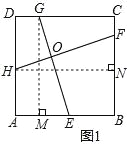
�����������1����G��GM��AB��M����H��HN��BC��N���������ε����ʺ;��ε�������GM=HN���������ı��ε��ڽǺ�Ϊ360�㣬�ɵá�DHO+��DGE=360��-90��-90��=180�㣬�á�HFN=��GEM����AAS������֤�á�GME�ա�HNF������ȫ�������ε����ʿɵý��ۣ�
��2����G��GM��AB��M����H��HN��BC��N�������ε����ʿɵ�DC=AB=BC��AD��BC��DC��AB���������ε������ʽ��GM=HN����AAS��������֤�á�GME�ա�HNF����ȫ�������ε����ʿɵý��ۣ�
��3����G��GM��AB��M����H��HN��BC��N������ƽ���ı��ε����ʺ������ʽ�ɵ�![]() ���á�GME�ס�HNF���������������ε����ʿɵò�����ȷ��
���á�GME�ס�HNF���������������ε����ʿɵò�����ȷ��
�����������1��EG=FH
�����ǣ���ͼ1����G��GM��AB��M����H��HN��BC��N��
���ı���ABCD�������Σ�
���D=��A=��B=��C=90�㣬
�֡�GM��AB��HN��BC
���ı���ADGM���ı���AHNB�Ǿ��Σ�
��HN=AB��AD=GM��
��HN=GM��
�ߡ�ADC=��HOE=90�㣬
���DHO+��DGE=360��-90��-90��=180�㣬
��AD��BC��DC��AB��
���NFH=��DHF����DGE+��GEM=180�㣬
���HFN=��GEM��
��HN��BC��GM��AB��
���GME=��HNF=90�㣬
�ڡ�GME�͡�HNF��
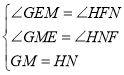 ��
��
���GME�ա�HNF��AAS����
��EG=FH��
��2��EG=FH��
�����ǣ���ͼ2����G��GM��AB��M����H��HN��BC��N��
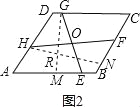
���ı���ABCD�����Σ�
��DC=AB=BC��AD��BC��DC��AB��
������ABCD�����S=AB��GM=BC��HN��
��GM=HN��
��GM��AB��HN��BC��
���GME=��HNF=90�㣬
�ߡ�ADC=��HOE��
���ADC+��HOG=��EOH+��HOG=180��
���DHO+��DGE=360��-180��=180�㣬
��AD��BC��DC��AB��
���NFH=��DHF����DGE+��GEM=180�㣬
���HFN=��GEM��
�ڡ�GME�͡�HNF��
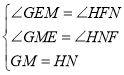 ��
��
���GME�ա�HNF��AAS����
��EG=FH��
��3����ȷ��
�����ǣ���ͼ3����G��GM��AB��M����H��HN��BC��N��
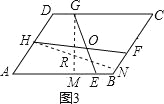
���ı���ABCD��ƽ���ı��Σ�
��AD��BC��DC��AB��
��ƽ���ı���ABCD�����S=AB��GM=BC��HN
��AB=a��AD=b��
��![]() ��
��
��GM��AB��HN��BC��
���GME=��HNF=90�㣬
�ߡ�ADC=��HOE��
���ADC+��HOG=��EOH+��HOG=180�㣬
���DHO+��DGE=360��-180��=180�㣬
��AD��BC��DC��AB��
���NFH=��DHF����DGE+��GEM=180�㣬
���HFN=��GEM��
���GME�ס�HNF��
��![]() ��
��

 ��У����ϵ�д�
��У����ϵ�д�