题目内容
如图所示,已知在直角梯形OABC中,AB∥OC,BC⊥x轴于点C、A(1,1)、B(3,1).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线OA,垂足为Q.设P点移动的时间为t秒(
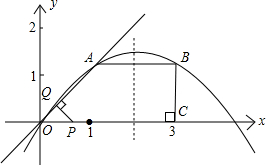
0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.
(1)求经过O、A、B三点的抛物线解析式;
(2)求S与t的函数关系式;
(3)将△OPQ绕着点P顺时针旋转90°,是否存在t,使得△OPQ的顶点O或Q在抛物线上?若存在,直接写出t的值;若不存在,请说明理由.
分析:(1)设抛物线解析式为y=ax2+bx,把已知坐标代入求出抛物线的解析式.
(2)求出S的面积,根据t的取值不同分三种情况讨论S与t的函数关系式.
(3)根据旋转的性质,代入解析式,判断是否存在.
解答:解:(1)方法一:由图象可知:抛物线经过原点,
设抛物线解析式为y=ax
2+bx(a≠0).
把A(1,1),B(3,1)代入上式得:(1分)
,
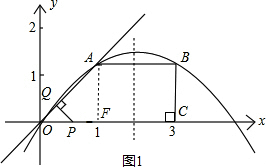
解得
.(3分)
∴所求抛物线解析式为y=-
x
2+
x.(4分)
方法二:∵A(1,1),B(3,1),
∴抛物线的对称轴是直线x=2.
设抛物线解析式为y=a(x-2)
2+h(a≠0)(1分)
把O(0,0),A(1,1)代入
得
,
解得
,(3分)
∴所求抛物线解析式为y=-
(x-2)
2+
.(4分)
(2)分三种情况:
①当0<t≤2,重叠部分的面积是S
△OPQ,过点A作AF⊥x轴于点F,
∵A(1,1),
∴在Rt△OAF中,AF=OF=1,∠AOF=45°,在Rt△OPQ中,OP=t,∠OPQ=∠QOP=45°,
∴PQ=OQ=tcos 45°=
t.S=
(t)2=t
2,(6分)
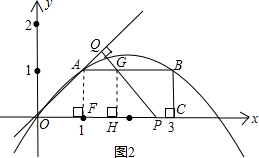
②当2<t≤3,设PQ交AB于点G,作GH⊥x轴于点H,∠OPQ=∠QOP=4
5°,
则四边形OAGP是等腰梯形,重叠部分的面积是S
梯形OAGP.
∴AG=FH=t-2,
∴S=
(AG+OP)AF=
(t+t-2)×1=t-1.(8分)
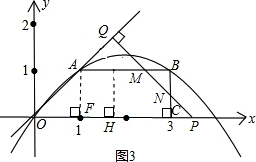
③当3<t<4,设PQ与AB交于点M,交BC于点N,重叠部分的面积是S
五边形OAMNC.
因为△PNC和△BMN都是等腰直角三角形,
所以重叠部分的面积是S
五边形OAMNC=S
梯形OABC-S
△BMN.
∵B(3,1),OP=t,
∴PC=CN=t-3,
∴S=
(2+3)×1-
(4-t)
2,
S=-
t
2+4t-
.(10分)
(3)存在.
当O点在抛物线上时,将O(t,t)代入抛物线解析式,解得t=0(舍去),t=1;
当Q点在抛物线上时,Q(
t,
t)代入抛物线解析式得t=0(舍去),t=2.
故t=1或2.
点评:本题是一道典型的综合题,重点考查了二次函数的有关知识以及考生理解图形的能力,难度较大.
练习册系列答案
相关题目
 0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.
0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.

 5°,
5°,

 5°,
5°,
 直于直线OA,垂足为Q,设P点移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.
直于直线OA,垂足为Q,设P点移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.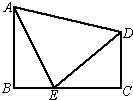 6、如图所示,已知在直角梯形ABCD中,∠B=∠C=90°,E为BC上的点,且EA=ED,∠AEB=75°,∠DEC=45°,试说明AB=BC.
6、如图所示,已知在直角梯形ABCD中,∠B=∠C=90°,E为BC上的点,且EA=ED,∠AEB=75°,∠DEC=45°,试说明AB=BC. 如图所示,已知在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,1)、B(3,1).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线OA,垂足为Q.设P点移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.
如图所示,已知在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,1)、B(3,1).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线OA,垂足为Q.设P点移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S. 如图所示,已知在直角三角形纸片ABC中,BC=3,∠BAC=30°,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )
如图所示,已知在直角三角形纸片ABC中,BC=3,∠BAC=30°,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )