题目内容
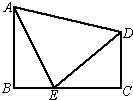 6、如图所示,已知在直角梯形ABCD中,∠B=∠C=90°,E为BC上的点,且EA=ED,∠AEB=75°,∠DEC=45°,试说明AB=BC.
6、如图所示,已知在直角梯形ABCD中,∠B=∠C=90°,E为BC上的点,且EA=ED,∠AEB=75°,∠DEC=45°,试说明AB=BC.分析:作AF⊥CD交CD的延长线于F,由∠AEB=75°,∠DEC=45°得∠AEB=60°,由EA=ED即可得△AED为等边三角形,即AE=AD;由∠AEB=75°AF⊥CD,可得∠BAE=∠FAD,则可得△ABE≌△AFD,得AB=AF;由条件可知四边形ABCF为矩形,即可得AB=BC.
解答:解:作AF⊥CD交CD的延长线于F,
∵∠AEB=75°,∠DEC=45°,
∴∠AED=60°,
又∵EA=ED,①
∴△AED为等边三角形,即AE=AD;
∵∠AEB=75°,AF⊥CD,
∴∠BAE=∠FAD=15°,②
由∠ABE=∠AFD=90°和结论①②可得△ABE≌△AFD(AAS),
∴AB=AF;③
∵∠B=∠C=90°,AF⊥CD,
∴四边形ABCF为矩形,即AF=BC,④
∴由结论③④可得AB=BC.
∵∠AEB=75°,∠DEC=45°,

∴∠AED=60°,
又∵EA=ED,①
∴△AED为等边三角形,即AE=AD;
∵∠AEB=75°,AF⊥CD,
∴∠BAE=∠FAD=15°,②
由∠ABE=∠AFD=90°和结论①②可得△ABE≌△AFD(AAS),
∴AB=AF;③
∵∠B=∠C=90°,AF⊥CD,
∴四边形ABCF为矩形,即AF=BC,④
∴由结论③④可得AB=BC.
点评:本题考查直角梯形的性质,涉及到全等三角形全等的判定知识点,作出正确的辅助线是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.
0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S. 直于直线OA,垂足为Q,设P点移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.
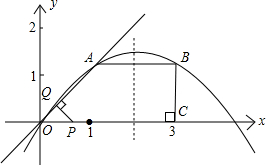
直于直线OA,垂足为Q,设P点移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S. 如图所示,已知在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,1)、B(3,1).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线OA,垂足为Q.设P点移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.
如图所示,已知在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,1)、B(3,1).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线OA,垂足为Q.设P点移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S. 如图所示,已知在直角三角形纸片ABC中,BC=3,∠BAC=30°,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )
如图所示,已知在直角三角形纸片ABC中,BC=3,∠BAC=30°,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )