题目内容
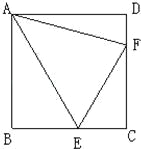
【题目】如图,D为ABC的AB边上一点,E为AC延长线上的一点,且CE=BD。
(1)当AB=AC时,求证:DE>BC
(2)当AB≠AC时,DE与BC有何大小关系?给出结论,画出图形,并证明。

【答案】(1)见解析;(2)见解析
【解析】试题分析:
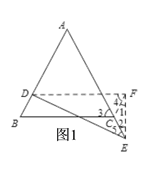
(1)如图1,过点D作DF∥BC,过点C作CF∥AB,连接EF,从而可得DF=BC,这样就把分散的线段集中到了△DEF中,只需证DE>DF即可;易证∠1=∠2,∠3=∠4,∠3>∠5,从而可得∠DFE>∠DEF,∴DE>DF,从而得到:DE>BC;
(2)当AB![]() AC时,我们要分AB>AC和AB<AC两种情况来讨论,
AC时,我们要分AB>AC和AB<AC两种情况来讨论,
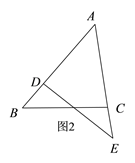
其中:①当AB>AC,且AB=AE时,如图2,结合已知条件此时我们易证△ABC≌△AED,从而得到BC=DE;
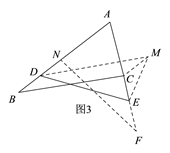
②当AB>AC,且AB>AE时,如图3,延长AE到F,使AF=AB,在AB上截取AN=AC,易证△ABC≌△AFN,得到∠F=∠B;再过D作DM∥BC,过C作CM∥BD,得到四边形DBCM是平行四边形,由此可得∠DMC=∠B=∠F,DM=BC;连接ME,则法通过在△DME中证∠DEM>∠DME得到DM>DE,从而得到BC>DE;
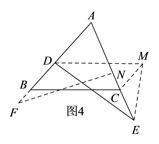
③当AB>AC,且AB<AE时,如图4,延长AB到F,使AF=AE,在AE上截取AN=AD,连接NF,易证△AFN≌△AED,可得∠F=∠AED,由∠ABC>∠F得到∠ABC>∠AED;再作DM∥BC,CM∥AB,可得四边形DBCM是平行四边形,得到DM=BC,∠DMC=∠ABC,就可得∠DMC>∠AED;连接ME,在△DME中通过证∠DME>∠DEM,得到DE>DM,就可得到DE>BC;
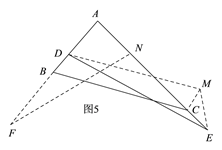
④当AB<AC<AE时,如图5,延长AB至F,使AF=AE,在AC上截取AN=AD;过点D作DM∥BC,过点C作CM∥AB,连接ME;同上可证:DE>BC.
试题解析:
(1)作DF∥BC,CF∥BD(如图1),
得□BCFD,从而∠DFC=∠B,
DF=BC,CF=BD.
又BD=CE,∴CF=CE,
∴∠1=∠2.
∵AB=AC,∴∠ACB=∠B.
而∠DFE=∠DFC+∠1=∠B+∠1
=∠ACB+∠2>∠AED+∠2=∠DEF,
即在△DEF中,∵∠DFE>∠DEF,
∴DE>DF,即DE>BC.
(2)当AB≠AC时,DE与BC的大小关系如下:
当AB>AC但AB=AE时,DE=BC;
当AB>AC且AB>AE时,DE<BC;
当AB>AC但AB<AE时,DE>BC;
当AB<AC时,DE>BC.
证明如下:
①当AB>AC但AB=AE时(如图2),
∵BD=CE,∴AB-BD=AE-CE,即AD=AC.
在△ABC和△AED中,
∵AB=AE,∠A=∠A,AC=AD,
∴△ABC≌△AED(SAS),∴BC=ED;
②当AB>AC且AB>AE时,
延长AE到F,使AF=AB,
在AB上截取AN=AC(如图3),连结NF.
在△ABC和△AFN中,
∵AB=AF,∠A=∠A,AC=AN,
∴△ABC≌△AFN(SAS),∴∠B=∠F.
∵∠AED>∠F,∴∠AED>∠B.
过D点作DM∥BC,过点C作CM∥AB,连结EM,
则四边形DBCM为平行四边形,∴∠DMC=∠B,CM=BD,DM=BC,
∵BD=CE,∴CM=CE,∴∠CME=∠CEM,
∵∠DMC=∠B<∠AED,∴∠CME+∠DMC<∠AED+∠CEM,
即∠DME<∠DEM,∴DE<DM,∴DE<BC;
③当AB>AC但AB<AE时,延长AB到F,使AF=AE,
在AE上截取AN=AD(如图4),连结NF,
在△AFN和△AED中,
∵AF=AE,∠A=∠A,AN=AD,
∴△AFN≌△AED(SAS),
∴∠F=∠AED,
∵∠ABC>∠F,
∴∠ABC>∠AED,
过D点作DM∥BC,过点C作CM∥AB,连接EM,
则四边形DBCM为平行四边形,
∴∠DMC=∠ABC,CM=BD,
∵BD=CE,
∴CM=CE,
∴∠CME=∠CEM,
∵∠DMC=∠ABC>∠AED,
∴∠DMC+∠CME>∠AED+∠CEM,
即∠DME>∠DEM,
∴ DE>DM,
∴ DE>BC;
④当AB<AC时,此时,AB必小于AE,即AB<AE
延长AB到F,使AF=AE,在AE上截取AN=AD(如图5).
连结NF.在△AFN和△AED中,
∵AF=AE,∠A=∠,AN=AD,∴△AFN≌△AED(SAS),
∴∠F=∠AED,即∠F=∠4.∵∠ABC>∠F,∴∠ABC>∠AED,
过D作DM∥BC,过点C作CM∥AB,连结CM,
则四边形DBCM平行四边形,∴∠DMC=∠ABC,CM=BD,DM=BC,
∵BD=CE,∴CM=CE,∴∠CME=∠CEM.∵∠DMC=∠ABC>∠AED,
∴∠DMC+∠CDE>∠AED+∠CEM,即∠DME>∠DEM,
∴DE>DM,
∴DE>BC.

 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案【题目】在一次大学生一年级新生训练射击比赛中,某小组的成绩如表
环数 | 6 | 7 | 8 | 9 |
人数 | 1 | 5 | 3 | 1 |
(1)该小组射击数据的众数是 .
(2)该小组的平均成绩为多少?(要写出计算过程)
(3)若8环(含8环)以上为优秀射手,在1200名新生中有多少人可以评为优秀射手?