题目内容
【题目】如图，在平面直角坐标系中，正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且相似比为 
，点A，B，E在x轴上，若正方形BEFG的边长为6，则点C的坐标为（ ）
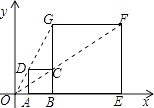
A.（2，2）
B.（3，1）
C.（3，2）
D.（4，2）
【答案】C
【解析】解：∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且相似比为 
，
∴ 
= ， 
= 
= ，
即 
= ， 
= ，
解得，OB=3，CD=2，
∴点C的坐标为（3，2），
所以答案是：C．
【考点精析】本题主要考查了正方形的性质和位似变换的相关知识点，需要掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形；它们具有相似图形的性质外还有图形的位置关系（每组对应点所在的直线都经过同一个点—位似中心）才能正确解答此题．
练习册系列答案
阅读快车系列答案
相关题目
