题目内容
【题目】如图,△ABC中,CE和CF分别平分∠ACB和△ABC的外角∠ACD,一动点O在AC上运动,过点O作BD的平行线与∠ACB和∠ACD的角平分线分别交于点E和点F.
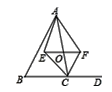
(1)求证:当点O运动到什么位置时,四边形AECF为矩形,说明理由;
(2)在第(1)题的基础上,当△ABC满足什么条件时,四边形AECF为正方形,说明理由.
【答案】(1)当点O运动到AC的中点位置时,四边形AECF为矩形,理由见解析;(2)当△ABC为直角三角形时,四边形AECF为正方形,理由见解析.
【解析】
(1)利用角平分线的性质以及平行线的性质得出OE=OF,即可得出结论;
(2)证出EF⊥AC,即可得出结论.
(1)证明:当点O运动到AC的中点位置时,四边形AECF为矩形;理由如下:
∵O为AC中点,
∴OA=OC,
∵EF∥BD,
∴∠CEO=∠ECB,
∵CE平分∠ACB,
∴∠BCE=∠ACE,
∴∠CEO=∠ECO,
∴OE=OC,
同理可证,OC=OF,
∴OE=OF,
∴四边形AECF为平行四边形,
又∵EF=2OE,AC=2OC,
∴EF=AC,
∴四边形AECF为矩形;
(2)解:当△ABC为直角三角形时,即∠ACB=90°时,四边形AECF为正方形;
理由如下:
∵EF∥BD,∠ACB=90°,
∴∠AOE=90°,
∴EF⊥AC,
∵四边形AECF为矩形,
∴四边形AECF为正方形.

【题目】下表是橘子的销售额随橘子卖出质量的变化表:
质量/千克 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | … |
销售额/元 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | … |
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当橘子卖出5千克时,销售额是_______元.
(3)如果用![]() 表示橘子卖出的质量,
表示橘子卖出的质量,![]() 表示销售额,按表中给出的关系,
表示销售额,按表中给出的关系,![]() 与
与![]() 之间的关系式为______.
之间的关系式为______.
(4)当橘子的销售额是100元时,共卖出多少千克橘子?