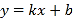题目内容
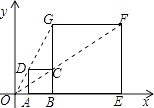
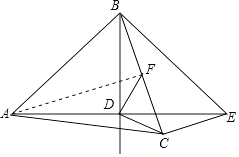
【题目】如图,在△ABC中,AB=AC,点D是△ABC内一点,AD=BD,且AD⊥BD,连接CD.过点C作CE⊥BC交AD的延长线于点 E,连接BE.过点D作DF⊥CD交BC于点F.
(1)若BD=DE= ![]() ,CE=
,CE= ![]() ,求BC的长;
,求BC的长;
(2)若BD=DE,求证:BF=CF.
【答案】
(1)解:∵BD⊥AD,点E在AD的延长线上,
∴∠BDE=90°,
∵BD=DE= ![]() ,
,
∴BE= ![]() =
= ![]() ,
,
∵BC⊥CE,
∴∠BCE=90°,
∴BC= ![]() =
= ![]() =2
=2 ![]()
(2)解:连接AF,
∵CD⊥BD,DF⊥CD,
∴∠BDE=∠CDF=90°,
∴∠BDF=∠CDE,
∵CE⊥BC,
∴∠BCE=90°,
∴∠DBC=∠CED,
在△BDF和△EDC中,
∵ 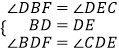 ,
,
∴△BDF≌△EDC(ASA),
∴DF=CD,
∴∠CFD=∠DCF=45°,
∵∠ADB=∠CDF,
∴∠ADB+∠BDF=∠CDF+∠BDF,
∴∠ADF=∠BDC,
在△ADF和△BDC中,
∵ 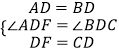 ,
,
∴△ADF≌△BDC(SAS),
∴∠AFD=∠BCD,
∴∠AFD=45°,
∴∠AFC=∠AFD+∠CFD=90°,
∴AF⊥BC,
∴AB=AC,
∴BF=CF
【解析】利用勾股定理可求出BE,进而求出BC;(2)要证线段相等,可证△BDF≌△EDC,为△ADF≌△BDC准备条件,证出BF=CF.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目