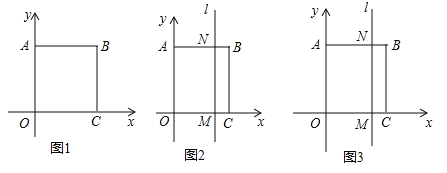
МвДїДЪИЭ
ЎѕМвДїЎїИзНјКѕЈ¬ТФХэ·ЅРО![]() µДµг
µДµг![]() ОЄЧш±кФµгЅЁБўЖЅГжЦ±ЅЗЧш±кПµЈ¬ЖдЦРПЯ¶О
ОЄЧш±кФµгЅЁБўЖЅГжЦ±ЅЗЧш±кПµЈ¬ЖдЦРПЯ¶О![]() ФЪ
ФЪ![]() ЦбЙПЈ¬ПЯ¶О
ЦбЙПЈ¬ПЯ¶О![]() ФЪ
ФЪ![]() ЦбЙПЈ¬ЖдЦРХэ·ЅРО
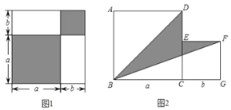
ЦбЙПЈ¬ЖдЦРХэ·ЅРО![]() µДЦЬі¤ОЄ24Ј®
µДЦЬі¤ОЄ24Ј®
ЈЁ1Ј©Ц±ЅУРґіц![]() Ј¬
Ј¬![]() БЅµгµДЧш±кЈ®
БЅµгµДЧш±кЈ®
ЈЁ2Ј©ИфУл![]() ЦбЦШєПµДЦ±ПЯ
ЦбЦШєПµДЦ±ПЯ![]() ТФГїГл1ёцµҐО»і¤¶ИµДЛЩ¶ИУЙ
ТФГїГл1ёцµҐО»і¤¶ИµДЛЩ¶ИУЙ![]() ЦбПтУТЖЅТЖЈ¬ТЖ¶ЇЦБУл
ЦбПтУТЖЅТЖЈ¬ТЖ¶ЇЦБУл![]() ЛщФЪµДЦ±ПЯЦШєПК±НЈЦ№Ј®ФЪТЖ¶Ї№эіМЦРЦ±ПЯ
ЛщФЪµДЦ±ПЯЦШєПК±НЈЦ№Ј®ФЪТЖ¶Ї№эіМЦРЦ±ПЯ![]() Ул
Ул![]() Ўў
Ўў![]() Ѕ»µг·Ц±рОЄµг
Ѕ»µг·Ц±рОЄµг![]() єНµг
єНµг![]() Ј®ОКЈєФЛ¶Ї¶аі¤К±јдК±Ј¬і¤·ЅРО
Ј®ОКЈєФЛ¶Ї¶аі¤К±јдК±Ј¬і¤·ЅРО![]() µДЦЬі¤Улі¤·ЅРО
µДЦЬі¤Улі¤·ЅРО![]() µДЦЬі¤Ц®±ИОЄ5Јє4Ј®
µДЦЬі¤Ц®±ИОЄ5Јє4Ј®
ЈЁ3Ј©ФЪЈЁ2Ј©µДМхјюПВЈ¬ИфЦ±ПЯ![]() ЙПУРТ»µг
ЙПУРТ»µг![]() Ј¬Б¬ЅУ
Ј¬Б¬ЅУ![]() Ўў
Ўў![]() Ј¬ЗЎєГВъЧг
Ј¬ЗЎєГВъЧг![]() Ј®Зуіц
Ј®Зуіц![]() µДґуРЎЈ®
µДґуРЎЈ®
Ўѕґр°ёЎїЈЁ1Ј©BЈЁ6,6Ј©Ј¬CЈЁ6,0Ј©Ј»ЈЁ2Ј©ФЛ¶Ї4ГлК±Ј¬і¤·ЅРО![]() µДЦЬі¤Улі¤·ЅРО
µДЦЬі¤Улі¤·ЅРО![]() µДЦЬі¤Ц®±ИОЄ5Јє4Ј»ЈЁ3Ј©
µДЦЬі¤Ц®±ИОЄ5Јє4Ј»ЈЁ3Ј©![]() ОЄ270Ўг»т90ЎгК±ЗЎєГ
ОЄ270Ўг»т90ЎгК±ЗЎєГ![]() .
.
ЎѕЅвОцЎї
ЈЁ1Ј©ёщѕЭХэ·ЅРОµДРФЦКјґїЙµГµЅOAЎўOCµДі¤¶ИУЙґЛµГµЅµгµДЧш±кЈ»
ЈЁ2Ј©ЙиТЖ¶ЇtГлЈ¬ёщѕЭЖЅТЖµГµЅAN=OM=tЈ¬MN=OA=6Ј¬ёщѕЭі¤·ЅРО![]() µДЦЬі¤Улі¤·ЅРО
µДЦЬі¤Улі¤·ЅРО![]() µДЦЬі¤Ц®±ИОЄ5Јє4БРіц·ЅіМЗуЅвјґїЙµГµЅґр°ёЈ»
µДЦЬі¤Ц®±ИОЄ5Јє4БРіц·ЅіМЗуЅвјґїЙµГµЅґр°ёЈ»
ЈЁ3Ј©·ЦБЅЦЦЗйїцЈєµгEФЪABЙП·Ѕ»тПВ·ЅК±Ј¬·Ц±р»НјЈ¬ёщѕЭґ№Ц±µД¶ЁТеј°Хэ·ЅРОµДРФЦКЗуЦµјґїЙ.
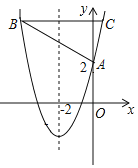
ЈЁ1Ј©ЎЯЛД±ЯРОABCOКЗХэ·ЅРОЈ¬ЗТЦЬі¤КЗ24Ј¬
ЎаOA=OC=AB=BC=6Ј¬ABЎНOAЈ¬BCЎНOCЈ¬
ЎаBЈЁ6,6Ј©Ј¬CЈЁ6,0Ј©Ј»
ЈЁ2Ј©ЙиТЖ¶ЇtГлЈ¬
ЎЯУл![]() ЦбЦШєПµДЦ±ПЯ
ЦбЦШєПµДЦ±ПЯ![]() ТФГїГл1ёцµҐО»і¤¶ИµДЛЩ¶ИУЙ
ТФГїГл1ёцµҐО»і¤¶ИµДЛЩ¶ИУЙ![]() ЦбПтУТЖЅТЖЈ¬
ЦбПтУТЖЅТЖЈ¬
ЎаAN=OM=tЈ¬MN=OA=6Ј¬
ЎаBN=CM=6-tЈ¬
ЎЯі¤·ЅРО![]() µДЦЬі¤Улі¤·ЅРО
µДЦЬі¤Улі¤·ЅРО![]() µДЦЬі¤Ц®±ИОЄ5Јє4Ј¬
µДЦЬі¤Ц®±ИОЄ5Јє4Ј¬
Ўа4ЈЁ2t+12Ј©=5ЈЁ12-2t+12Ј©Ј¬
ЅвµГt=4Ј¬
Ўаµ±Ц±ПЯlФЛ¶Ї4ГлК±Ј¬і¤·ЅРО![]() µДЦЬі¤Улі¤·ЅРО
µДЦЬі¤Улі¤·ЅРО![]() µДЦЬі¤Ц®±ИОЄ5Јє4Ј»
µДЦЬі¤Ц®±ИОЄ5Јє4Ј»
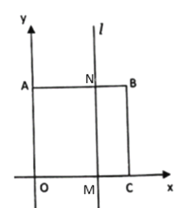
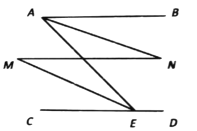
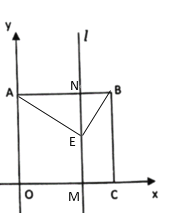
ЈЁ3Ј©µ±µгEФЪABЙП·ЅК±Ј¬ИзНјЈ¬
ЎЯ![]() Ј¬
Ј¬
ЎаЎПAEB=90ЎгЈ¬
ЎаЎПEAB+ЎПEBA=90ЎгЈ¬
ЎЯЛД±ЯРОABCOКЗХэ·ЅРОЈ¬
ЎаЎПOAB=ЎПABC=90ЎгЈ¬
Ўа![]() =ЎПOAB+ЎПEAB+ЎПABC+ЎПEBA=270ЎгЈ»
=ЎПOAB+ЎПEAB+ЎПABC+ЎПEBA=270ЎгЈ»
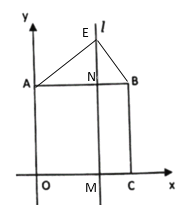
µ±µгEФЪABПВ·ЅК±Ј¬ИзНјЈ¬
ЎЯ![]() Ј¬
Ј¬
ЎаЎПAEB=90ЎгЈ¬
ЎаЎПEAB+ЎПEBA=90ЎгЈ¬
ЎЯЛД±ЯРОABCOКЗХэ·ЅРОЈ¬
ЎаЎПOAB=ЎПABC=90ЎгЈ¬
Ўа![]() =ЎПOAB-ЎПEAB+ЎПABC-ЎПEBA=90ЎгЈ»
=ЎПOAB-ЎПEAB+ЎПABC-ЎПEBA=90ЎгЈ»
ЧЫЙПЈ¬![]() ОЄ270Ўг»т90ЎгК±ЗЎєГ
ОЄ270Ўг»т90ЎгК±ЗЎєГ![]() .
.

 їОМГИ«ЅвЧЦґКѕд¶ОЖЄХВПµБРґр°ё
їОМГИ«ЅвЧЦґКѕд¶ОЖЄХВПµБРґр°ё ІЅІЅёЯїЪЛгМвїЁПµБРґр°ё
ІЅІЅёЯїЪЛгМвїЁПµБРґр°ё