题目内容
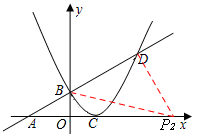
如图,已知一次函数 的图象与x轴交于点A,与二次函数
的图象与x轴交于点A,与二次函数 的图象交于y轴上的一点B,二次函数
的图象交于y轴上的一点B,二次函数 的图象与x轴只有唯一的交点C,且OC=2.
的图象与x轴只有唯一的交点C,且OC=2.

(1)求二次函数 的解析式;
的解析式;
(2)设一次函数 的图象与二次函数
的图象与二次函数 的图象的另一交点为D,已知P为x轴上的一个动点,且△PBD为直角三角形,求点P的坐标.
的图象的另一交点为D,已知P为x轴上的一个动点,且△PBD为直角三角形,求点P的坐标.
 的图象与x轴交于点A,与二次函数
的图象与x轴交于点A,与二次函数 的图象交于y轴上的一点B,二次函数
的图象交于y轴上的一点B,二次函数 的图象与x轴只有唯一的交点C,且OC=2.
的图象与x轴只有唯一的交点C,且OC=2.
(1)求二次函数
 的解析式;
的解析式;(2)设一次函数
 的图象与二次函数
的图象与二次函数 的图象的另一交点为D,已知P为x轴上的一个动点,且△PBD为直角三角形,求点P的坐标.
的图象的另一交点为D,已知P为x轴上的一个动点,且△PBD为直角三角形,求点P的坐标.(1)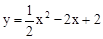 (2)P1(1,0)和P2(
(2)P1(1,0)和P2(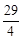 ,0)
,0)
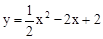 (2)P1(1,0)和P2(
(2)P1(1,0)和P2(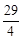 ,0)
,0)解:(1)∵ 交x轴于点A,∴0=0.5x+2,解得x=-4。∴A点坐标为:(-4,0)。
交x轴于点A,∴0=0.5x+2,解得x=-4。∴A点坐标为:(-4,0)。
∵ 与y轴交于点B,∴y=2。∴B点坐标为:(0,2)。
与y轴交于点B,∴y=2。∴B点坐标为:(0,2)。
∵二次函数 的图象与x轴只有唯一的交点C,且OC=2
的图象与x轴只有唯一的交点C,且OC=2
∴可设二次函数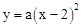 。
。
把B(0,2)代入得:a=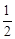 。
。
∴二次函数的解析式为: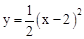 ,即
,即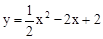 。
。
(2)①当B为直角顶点时,过B作BP1⊥AD交x轴于P1点,

∵Rt△AOB∽Rt△BOP1,∴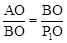 。
。
∴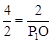 ,解得:OP1=1。
,解得:OP1=1。
∴P1点坐标为(1,0),
②当D为直角顶点时作P2D⊥BD,连接BP2,
将 与
与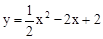 2联立求出两函数另一交点坐标:D点坐标为:(5,
2联立求出两函数另一交点坐标:D点坐标为:(5,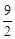 ),则AD=
),则AD=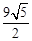 。
。
由A(-4,0),B(0,2)可得AB=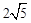 。
。
∵∠DAP2=∠BAO,∠BOA=∠ADP2,
∴△ABO∽△AP2D。∴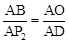 。
。
∴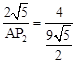 ,解得AP2=
,解得AP2=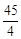 。
。
则OP2=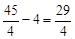 。
。
∴P2点坐标为(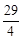 ,0)。
,0)。
③当P为直角顶点时,过点D作DE⊥x轴于点E,设P3(a,0),
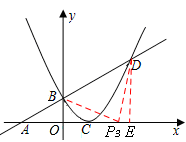
则由Rt△OBP3∽Rt△EP3D得: ,
,
∴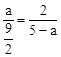 。
。
∵方程无解,∴点P3不存在。
综上所述,点P的坐标为:P1(1,0)和P2(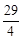 ,0)。
,0)。
(1)根据 交x轴于点A,与y轴交于点B,即可得出A,B两点坐标,二次函数
交x轴于点A,与y轴交于点B,即可得出A,B两点坐标,二次函数 的图象与x轴只有唯一的交点C,且OC=2.得出可设二次函数
的图象与x轴只有唯一的交点C,且OC=2.得出可设二次函数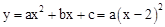 ,进而求出即可。
,进而求出即可。
(2)分点B为直角顶点,点D为直角顶点,点P为直角顶点三种情况讨论,分别利用三角形相似对应边成比例求出即可。
 交x轴于点A,∴0=0.5x+2,解得x=-4。∴A点坐标为:(-4,0)。
交x轴于点A,∴0=0.5x+2,解得x=-4。∴A点坐标为:(-4,0)。∵
 与y轴交于点B,∴y=2。∴B点坐标为:(0,2)。
与y轴交于点B,∴y=2。∴B点坐标为:(0,2)。∵二次函数
 的图象与x轴只有唯一的交点C,且OC=2
的图象与x轴只有唯一的交点C,且OC=2∴可设二次函数
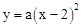 。
。把B(0,2)代入得:a=
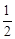 。
。∴二次函数的解析式为:
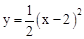 ,即
,即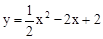 。
。(2)①当B为直角顶点时,过B作BP1⊥AD交x轴于P1点,

∵Rt△AOB∽Rt△BOP1,∴
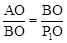 。
。∴
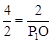 ,解得:OP1=1。
,解得:OP1=1。∴P1点坐标为(1,0),
②当D为直角顶点时作P2D⊥BD,连接BP2,

将
 与
与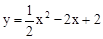 2联立求出两函数另一交点坐标:D点坐标为:(5,
2联立求出两函数另一交点坐标:D点坐标为:(5,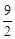 ),则AD=
),则AD=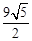 。
。由A(-4,0),B(0,2)可得AB=
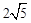 。
。∵∠DAP2=∠BAO,∠BOA=∠ADP2,
∴△ABO∽△AP2D。∴
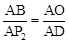 。
。∴
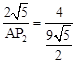 ,解得AP2=
,解得AP2=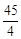 。
。则OP2=
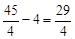 。
。∴P2点坐标为(
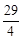 ,0)。
,0)。③当P为直角顶点时,过点D作DE⊥x轴于点E,设P3(a,0),

则由Rt△OBP3∽Rt△EP3D得:
 ,
,∴
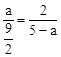 。
。∵方程无解,∴点P3不存在。
综上所述,点P的坐标为:P1(1,0)和P2(
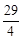 ,0)。
,0)。(1)根据
 交x轴于点A,与y轴交于点B,即可得出A,B两点坐标,二次函数
交x轴于点A,与y轴交于点B,即可得出A,B两点坐标,二次函数 的图象与x轴只有唯一的交点C,且OC=2.得出可设二次函数
的图象与x轴只有唯一的交点C,且OC=2.得出可设二次函数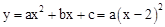 ,进而求出即可。
,进而求出即可。(2)分点B为直角顶点,点D为直角顶点,点P为直角顶点三种情况讨论,分别利用三角形相似对应边成比例求出即可。

练习册系列答案
相关题目


 垂直的直线l5的函数表达式.
垂直的直线l5的函数表达式.



 (k≠0),它们在同一坐标系中的大致图象为
(k≠0),它们在同一坐标系中的大致图象为