题目内容
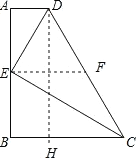
【题目】已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,![]() .E是边AB的中点,联结DE、CE,且DE⊥CE.设AD=x,BC=y.
.E是边AB的中点,联结DE、CE,且DE⊥CE.设AD=x,BC=y.
(1)如果∠BCD=60°,求CD的长;
(2)求y关于x的函数解析式,并写出自变量x的取值范围;
(3)联结BD.如果△BCD是以边CD为腰的等腰三角形,求x的值.
【答案】(1)4; (2)x>0,且![]() ; (3)
; (3)![]()
【解析】(1)首先过点D作DH⊥BC,垂足为点H,由AD∥BC,AB⊥BC,DH⊥BC,可求得DH的长,然后设CH=x,则 CD=2x,利用勾股定理即可求得方程:x2+(2![]()
![]() )2=4x2,解此方程即可求得答案;
)2=4x2,解此方程即可求得答案;
(2)首先取CD的中点F,连接EF,由梯形的中位线,可表示出EF的长,易得四边形ABHD是平行四边形,然后由勾股定理可得:(y﹣x)2+12=(x+y)2,继而求得答案;
(3)分别从CD=BD或CD=BC去分析求解即可求得答案.
解:(1)过点D作DH⊥BC,垂足为点H.
∵AD∥BC,AB⊥BC,DH⊥BC,
∴DH=AB=2![]() ,
,
在Rt△DHC中,
∵∠BCD=60°,
∴∠CDH=30°.
∴CD=2CH,
设CH=x,则 CD=2x.
利用勾股定理,得 CH2+DH2=CD2.
即得:x2+(2![]() )2=4x2.
)2=4x2.
解得 x=2(负值舍去).
∴CD=4;
(2)取CD的中点F,连接EF,
∵E为边AB的中点,
∴EF=![]() (AD+BC)=
(AD+BC)=![]() (x+y).
(x+y).
∵DE⊥CE,
∴∠DEC=90°.
又∵DF=CF,
∴CD=2EF=x+y.
由AB⊥BC,DH⊥BC,得∠B=∠DHC=90°.
∴AB∥DH.
又∵AB=DH,
∴四边形ABHD是平行四边形.
∴BH=AD=x.
即得 CH=|y﹣x|,
在Rt△DHC中,利用勾股定理,得 CH2+DH2=CD2.
即得 (y﹣x)2+12=(x+y)2.
解得![]() ,
,
∴所求函数解析式为![]() .
.
自变量x的取值范围是x>0,且![]() ;
;
(3)当△BCD是以边CD为腰的等腰三角形时,有两种可能情况:CD=BD或CD=BC.
( i)如果CD=BD,由DH⊥BC,得 BH=CH.即得 y=2x.
利用![]() ,得
,得![]() .
.
解得![]() ,
,![]() .
.
经检验:![]() ,
,![]() ,且
,且![]() 不合题意,舍去.
不合题意,舍去.
∴![]() ;
;
( ii)如果CD=BC,则 x+y=y.
即得 x=0(不合题意,舍去),
综上可得:![]() .
.
“点睛”此题属于四边形的综合题.考查了梯形的性质、平行四边形的判定与性质、等腰三角形的性质以及勾股定理等知识.注意掌握辅助线的作法,掌握方程思想与分类讨论思想的应用是解此题的关键.

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案