题目内容
【题目】已知:如图,在□ABCD中,E为边CD的中点,联结AE并延长,交边BC的延长线于点F.
(1)求证:四边形ACFD是平行四边形;
(2)如果∠B+∠AFB=90°,求证:四边形ACFD是菱形.
【答案】(1)(2)见解析
【解析】(1)根据平行四边形的性质证出∠ADC=∠FCD,然后再证明△ADE≌△FCE可得AD=FC,根据一组对边平行且相等的四边形是平行四边形可得结论;
(2)根据∠B+∠AFB=90°可得∠BAF=90°,根据平行四边形对边平行可得AB∥CD,利用平行线的性质可得∠CEF=∠BAF=90°,再根据对角线互相垂直的平行四边形是菱形可得结论.
证明:(1)在□ABCD中,AD∥BF.
∴∠ADC=∠FCD.
∵E为CD的中点,
∴DE=CE.
在△ADE和△FCE中,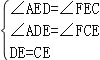 ,
,
∴△ADE≌△FCE(ASA)
∴AD=FC.
又∵AD∥FC,
∴四边形ACFD是平行四边形.
(2)在△ABF中,
∵∠B+∠AFB=90°,
∴∠BAF=90°.
又∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠CEF=∠BAF=90°,
∵四边形ACDF是平行四边形,
∴四边形ACDF是菱形.

练习册系列答案
相关题目