��Ŀ����
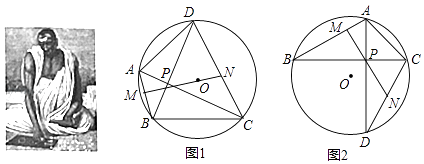
����Ŀ��ɽ����ɽ���й���ʷ�Ļ���ɽ������ʱ�ڽ���������Яĸ�����ڴ˱��ٶ����ƣ���ͼ1������ɽ�Ͻ�����ĸ�ӵ�����ij�οͼƻ�������������ĸ߶ȣ������ο���ֱ�ӵ�������ײ�����˸��οͼƻ���������߶�����������ĸ߶ȣ���ͼ2����������ɽ���½�A���������ͷ��C������Ϊ75�㣬����A������������10����P��ʱ���������ͷ��C�����Ǹպ�Ϊ45�㣬��֪ɽ�µ��¶�i=1��3����O��A��B��ͬһֱ���ϣ�������ĸ߶ȣ����������߶Ⱥ��Բ��ƣ������ȷ��0.1�ף��ο����ݣ�cos75���0.3��tan75���3.7�� ![]() ��1.4��
��1.4�� ![]() ��1.7��
��1.7�� ![]() ��3.2��
��3.2��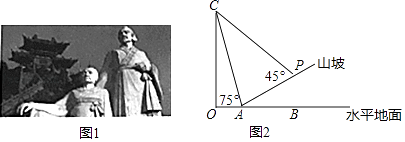
���𰸡��⣺����P��PE��OB�ڵ�E��PF��OC�ڵ�F��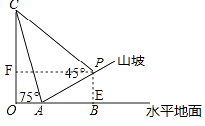
��i=1��3��AP=10��
��PE=x����AE=3x��
��Rt��AEP��x2+��3x��2=102 ��
��ã�x= ![]() ��x=��
��x=�� ![]() ���ᣩ��
���ᣩ��
��PE= ![]() ����AE=3
����AE=3 ![]() ��
��
�ߡ�CPF=��PCF=45�㣬
��CF=PF��
��CF=PF=m�ף���OC=��m+ ![]() ���ף�OA=��m��3
���ף�OA=��m��3 ![]() ���ף�
���ף�
��Rt��AOC��tan75��= ![]() =
= ![]() ����m+
����m+ ![]() =tan75�㣨m��3
=tan75�㣨m��3 ![]() ����
����
��ã�m��14.3��
��OC=14.3+ ![]() ��17.5�ף�
��17.5�ף�
������ĸ߶�ԼΪ17.5��
������������P��PE��OB�ڵ�E��PF��OC�ڵ�F����PE=x����AE=3x����Rt��AEP�и��ݹ��ɶ����ɵ�PE= ![]() ����AE=3
����AE=3 ![]() ����CF=PF=m�ף���OC=��m+
����CF=PF=m�ף���OC=��m+ ![]() ���ס�OA=��m��3
���ס�OA=��m��3 ![]() ���ף���Rt��AOC�У���tan75��=
���ף���Rt��AOC�У���tan75��= ![]() ���m��ֵ���̶��ɵô𰸣�
���m��ֵ���̶��ɵô𰸣�
�����㾫����������Ҫ�����˹����¶��½�����������Ǹ�����������֪ʶ�㣬��Ҫ���������Ǧֱ�߶�h��ˮƽ����l�ıȽ����¶�(�±�)������ĸi��ʾ����i=h/l����������ˮƽ��ļнǼ���A(�����½�)����ôi=h/l=tanA�����ǣ�������ˮƽ���Ϸ��Ľǣ����ǣ�������ˮƽ���·��ĽDz�����ȷ�����⣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�