题目内容
【题目】已知△ABC三边长a=b=6
，c=12．
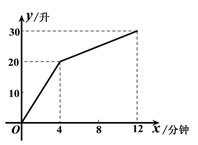
（1）如图1，以点A为原点，AB所在直线为x轴建立平面直角坐标系，直接出点B，C的坐标．
（2）如图2，过点C作∠MCN=45°交AB于点M，N，请证明AM2+BN2=MN2；
（3）如图3，当点M，N分布在点B异侧时，则（3）中的结论还成立吗？
【答案】（1）点C的坐标为（6，6）；（2）见解析；（3）仍然成立.
【解析】
（1）利用勾股定理逆定理判断出是直角三角形，从而得到△ABC是等腰直角三角形，再根据等腰直角三角形的性质求出点C的横坐标与纵坐标即可得解；
（2）把△ACM绕点C逆时针旋转90°得到△BCM′，连接M′N，根据旋转的性质可得AM=BM′、CM=CM′、∠CAM=∠CBM′，∠ACM=∠BCM′，然后求出∠MCN=∠M′CN，∠M′BN=90°，再利用“边角边”证明△MCN和△M′CN全等，根据全等三角形对应边相等可得MN=M′N，然后利用勾股定理列式证明即可；
（3）把△BCN绕点C顺时针旋转90°得到△ACN′，根据旋转的性质可得AN′=BN，CN′=CN，∠CAN′=∠CBN，然后判断出点N′在y轴上，再求出∠MCN′=45°，从而得到∠MCN=∠MCN′，再利用“边角边”证明△MCN和△MCN′全等，根据全等三角形对应边相等可得MN=MN′，然后利用勾股定理列式即可得证．
（1）∵a=b=6
，c=12，
∵a2+b2=（6）2+（6）2=144=c2，
∴△ABC是直角三角形，
又∵a=b，
∴△ABC是等腰直角三角形；
∵AB=c=12，
∴点B（12，0），
如图1，过点C作CD⊥x轴于D，
则AD=CD=
AB=×12=6，
∴点C的坐标为（6，6）；
（2）如图，把△ACM绕点C逆时针旋转90°得到△BCM′，连接M′N，
由旋转的性质得，AM=BM′、CM=CM′、∠CAM=∠CBM′=45°，∠ACM=∠BCM′，
∴∠M′BN=∠ABC+∠CBN′=45°+45°=90°，
∵∠MCN=45°，
∴∠M′CN=∠BCN+∠BCM′=∠BCN+∠ACM=90°﹣∠MCN=90°﹣45°=45°，
∴∠MCN=∠M′CN，
在△MCN和△M′CN中，
∵
，
∴△MCN≌△M′CN（SAS），
∴MN=M′N，
在Rt△M′NB中，BM′2+BN2=M′N2，
∴AM2+BN2=MN2；
（3）仍然成立，
如图3，∵△ABC是等腰直角三角形，
∴∠CAB=∠CBA=45°，
把△BCN绕点C顺时针旋转90°得到△ACN′，
由旋转的性质得，AN′=BN，CN′=CN，∠CAN′=∠CBN=135°，
∴∠MAN′=135°﹣45°=90°，
∴点N′在y轴上，
∵∠MCN=45°，
∴∠MCN′=90°﹣45°=45°，
∴∠MCN=∠MCN′，
在△MCN和△MCN′中，
∵
，
∴△MCN≌△MCN′（SAS），
∴MN=MN′，
在Rt△AMN′中，AM2+AN′2=MN′2，
∴AM2+BN2=MN2．
